





Цель работы
наблюдение перехода вертикальных колебаний пружинного маятника в крутильные и наоборот, измерение периодов вертикальных и крутильных колебаний, исследование их зависимости от параметров маятника.
Введение
Крутильные колебания можно наблюдать следующим образом.
Придадим
движение
маятнику Уилберфорса в вертикальном направлении. Возникнут обычные вертикальные
колебания, и их амплитуда с течением времени будет уменьшаться. Но одновременно
возникнут и крутильные колебания, и их амплитуда со временем будет увеличиваться.
При достижении максимума амплитуды крутильных колебаний, вертикальные
колебания прекратятся. Далее, амплитуда крутильных колебаний будет уменьшаться,
при этом амплитуда вертикальных колебаний увеличивается. Такое движение
может повторяться многократно. Возникают так называемые связанные
колебания и наблюдаются
биения в системе.
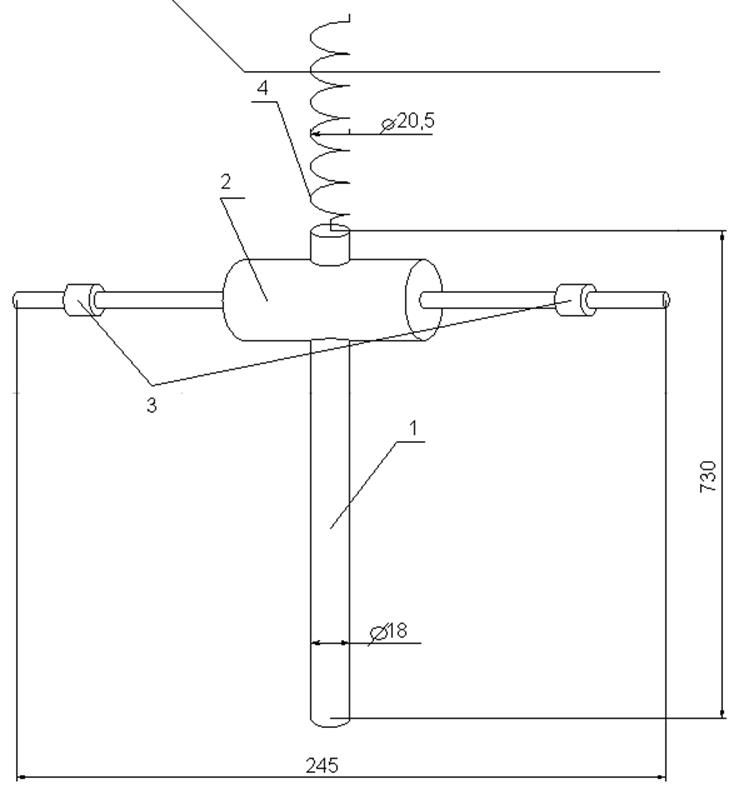
Экспериментальная установка для изучения колебаний маятника Уилберфорса показана на рисунке (4 - витая пружина, 2 - поперечный стержень с грузиками 3, 1 - стержень). На нем приведены геометрические параметры маятника.
Конструкция груза обеспечивает устойчивость к колебаниям вокруг горизонтальной оси и позволяет изменять момент инерции груза относительно вертикальной оси. Перемещая грузики по поперечному стержню, можно изменять частоту крутильных колебаний, не изменяя частоту вертикальных колебаний. Таким образом, можно исследовать движение системы при различных соотношениях частот вертикальных и крутильных колебаний.
Расчет некоторых механических характеристик системы и теоретических величин
Задание 1. Определяем числовые коэффициенты инерции из выражения (2). Очевидно, что масса груза складывается из массы стержня, массы поперечного стержня и масс двух грузиков:
а11=m=mcт+mnn+2mгр
а11=1,59 + 0,03+2·0,045=1,71 кг
Момент инерции системы складывается из момента инерции стержня относительно продольной оси, момента инерции поперечного стержня относительно центра масс и моментов инерции двух грузиков:
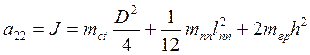
|
h, м |
0,02 |
0,04 |
0,06 |
0,08 |
0,1 |
|
a22 10-4, кг∙м2 |
3,489 |
4,569 |
6,369 |
8,889 |
12,129 |
Задание 2. Определяем коэффициенты жесткости из выражения (11):
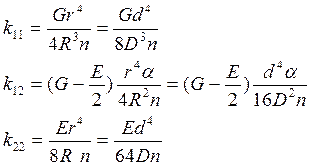
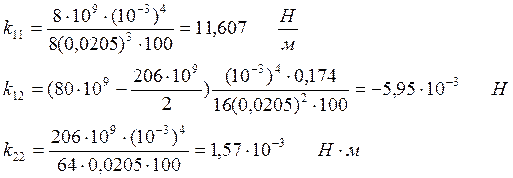
Величина коэффициента к12 отрицательна. Это означает что связь между координатами следующая: если увеличивать одну из координат, то другая координата уменьшается. Другими словами - если пружину удлинять, то она раскручивается, а если ее закручивать, то – укорачивается.
Необходимое условие существование биения (см.
теоретическую часть формула 28),имеет вид: ![]() .
.
В нашем случае имеем: ![]()
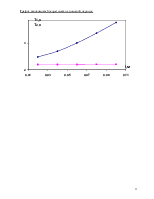
Определяем частоты ω1 и ω2 , используя формулы (16):
|
h, м |
0,02 |
0,04 |
0,06 |
0,08 |
0,1 |
|
ω 1, рад/с |
2,115 |
1,85 |
1,568 |
1,327 |
1,136 |
|
ω 2, рад/с |
2,61 |
2,608 |
2,607 |
2,606 |
2,606 |
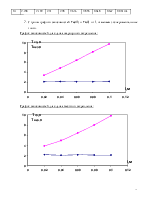
Зная частоты мы можем рассчитать и теоретические значения
для периодов по формуле :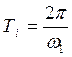 .
.
|
h, м |
0,02 |
0,04 |
0,06 |
0,08 |
0,1 |
|
Т1, с |
2,97 |
3,396 |
4,007 |
4,735 |
5,531 |
|
Т 2, с |
2,407 |
2,409 |
2,41 |
2,411 |
2,411 |
Эти числовые значения частот являются приближенными, в частности, из-за того, что модули упругости Eи Gпроволоки данной пружины точно неизвестны. При определении частот также не учитывалась инерционность пружины (массой пружины пренебрегли).
Для измерения периодов колебаний используется цифровой секундомер с ценой наименьшего деления 0,001 с.
Параметры установки представлены в таблице 1. Пружина навита из стальной проволоки с механическими параметрами: E=206∙109 Па, G=80∙109 , α=0,174 рад
Таблица 1
|
Параметр |
Числовое значение |
|
Масса стержня без пружины тсt |
1,55 кг |
|
Масса стержня с пружиной тct2 |
1,59 кг |
|
Масса поперечного стержня тпп |
30∙10-3 кг |
|
Масса одного грузика тгр |
45∙10-3 кг |
|
Число витков пружины п |
100 |
|
Длина стержня lct |
0.73 м |
|
Диаметр стержня dct |
0.018 м |
|
Длина поперечного стержня lпп |
0.245 м |
|
Диаметр пружины D |
0.0205 м |
|
Диаметр проволоки пружины d |
0.001 м |
Проведение эксперимента
1. Выбираем на половине поперечника пять одинаково удаленных друг от друга точек. Каждая такая точка находится на некотором расстоянии от вертикальной оси стержня. Переместим каждый грузик вдоль поперечного стержня на определенное расстояние, соответствующее первой точке, от вертикальной оси стержня.
2. Измеряем период вертикальных колебаний маятника. Для этого приводим маятник в движение (оттянув вниз и отпустив). Для точности проводим 3 таких измерений и заносим данные в таблицу 2. Проводим эксперимент для двух видов закрепления: шарнирного и жесткого.
Таблица 2
|
№ |
L, м |
Число полных колебаний |
t, c |
Тверт, с |
||
|
шарнирно |
жестко |
шарнирно |
жестко |
|||
|
1 |
0.02 |
5 |
9.4 |
11.00 |
1.88 |
2.2 |
|
2 |
11.17 |
10.89 |
2.234 |
2.178 |
||
|
3 |
10.94 |
10.99 |
2.188 |
2.198 |
||
|
1 |
0.04 |
5 |
10.74 |
10.49 |
2.148 |
2.098 |
|
2 |
10.4 |
10.3 |
2.08 |
2.06 |
||
|
3 |
10.81 |
10.5 |
2.162 |
2.1 |
||
|
1 |
0.06 |
5 |
10.64 |
10.82 |
2.128 |
2.164 |
|
2 |
10.14 |
10.95 |
2.028 |
2.19 |
||
|
3 |
10.56 |
10.64 |
2.112 |
2.128 |
||
|
1 |
0.08 |
5 |
10.31 |
10.5 |
2.062 |
2.1 |
|
2 |
10.84 |
10.59 |
2.168 |
2.118 |
||
|
3 |
10.32 |
10.6 |
2.064 |
2.12 |
||
|
1 |
0.1 |
5 |
11.01 |
10.57 |
2.202 |
2.114 |
|
2 |
10.75 |
10.54 |
2.15 |
2.108 |
||
|
3 |
10.61 |
10.52 |
2.122 |
2.104 |
||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.