Физика \ Физика

Наблюдение перехода вертикальных колебаний пружинного маятника в крутильные и наоборот, измерение периодов вертикальных и крутильных колебаний, страница 2

Измеряем период крутильных колебаний маятника. Для этого приводим маятник в движение (закручиваем поперечный стержень на 5 оборотов), данные эксперимента заносим в таблицу 3.

Таблица 3.

№	L, м	Число полных колебаний	t, c		Т_кр, с
№	L, м	Число полных колебаний	шарнирно	жестко	шарнирно	жестко
1	0.02	5	17.45	19.31	3.49	3.862
2			16.64	19.51	3.328	3.902
3			16.62	19.71	3.324	3.942
1	0.04	5	24.48	24.72	4.896	4.944
2			22.61	24.96	4.522	4.992
3			25.48	25.03	5.096	5.006
1	0.06	5	32.33	32.64	6.466	6.528
2			32.07	32.10	6.414	6.42
3			31.75	32.16	6.35	6.432
1	0.08	5	40.88	40.45	8.176	8.09
2			40.29	40.88	8.058	8.176
3			40.57	39.19	8.144	7.838
1	0.1	5	48.33	48.73	9.76	9.746
2			48.61	49.49	9.722	9.898
3			48.43	49.60	9.686	9.92

4. Производим обработку значения вертикальных колебаний из таблицы 2 и значения крутильных колебаний из таблицы 3 и получаем соответствующие Т_вер и Т_кр, а также их погрешности. Для этого используем следующие формулы :

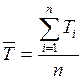- среднее значение;

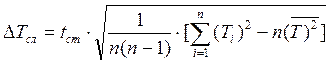- случайная погрешность;

- полная погрешность измерения.

Здесь n – число измерений, t_Ст – коэффициент Стьюдента для n измерений, с – систематическая погрешность (определяется половиной цены наименьшего деления секундомера).

Вертикальные периоды колебаний:

l, м			ΔТ_сл		ΔТ
l, м	шарнирно	жестко	шарнирно	жестко	шарнирно	жестко
0,02	2,1	2,192	0,2613	0,016	0,27	0,0167
0,04	2,13	2,086	0,056	0,029	0,0562	0,0294
0,06	2,089	2,161	0,092	0,045	0,0921	0,0453
0,08	2,098	2,113	0,078	0,056	0,0782	0,0562
0,1	2,158	2,109	0,051	0,058	0,0512	0,0582

Крутильные периоды колебаний:

l, м			ΔТ_сл		ΔТ
l, м	шарнирно	жестко	шарнирно	жестко	шарнирно	жестко
0,02	3,381	3,902	0,096	0,051	0,0961	0,0512
0,04	4,838	4,981	0,375	0,08	0,375	0,0802
0,06	6,41	6,46	0,074	0,194	0,0742	0,194
0,08	8,116	8,035	0,076	0,194	0,0762	0,194
0,1	9,693	9,855	0,123	0,038	0,1231	0,0383

5. Находим угловые частоты, соответствующие периодам Т_вер, и Т_кр по формулам:

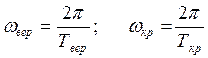
6. Находим момент инерции системы I_систпо формуле:

J=I_сист=I_ст+I_пп+I_гр

Здесь

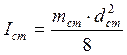- момент инерции вертикального стержня,

- момент инерции поперечного стержня,

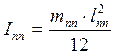- момент инерции двух грузиков.

Все полученные результаты заносим в таблицу 4.

l,м	вертикальные				крутильные				I_сист, кг·м²
	Т,с		ω, с^-1		Т, с		ω, с^-1
	шарнирно	жестко	шарнирно	жестко	шарнирно	жестко	шарнирно	жестко
0,02	2,1	2,192	2,99	2,866	3,381	3,902	1,858	1,61	0,0002505
0,04	2,13	2,086	2,95	3,012	4,838	4,981	1,299	1,26	0,0003585
0,06	2,089	2,161	3	2,907	6,41	6,46	0,98	0,97	0,0005385
0,08	2,098	2,113	2,99	2,97	8,116	8,035	0,774	0,78	0,0007905
0,1	2,158	2,109	2,91	2,98	9,693	9,855	0,648	0,637	0,001114

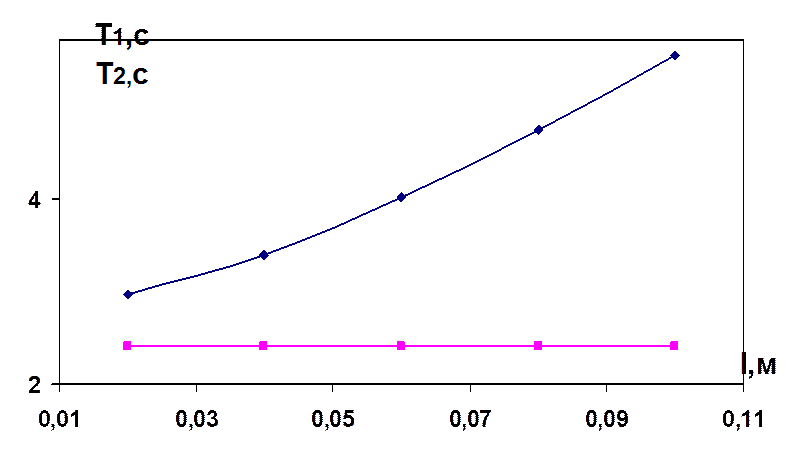
7. Строим графики зависимостей Т_верт(l) и Т_кр(l) от l, отмечаем экспериментальные точки.

График зависимостей для случая шарнирного закрепления:

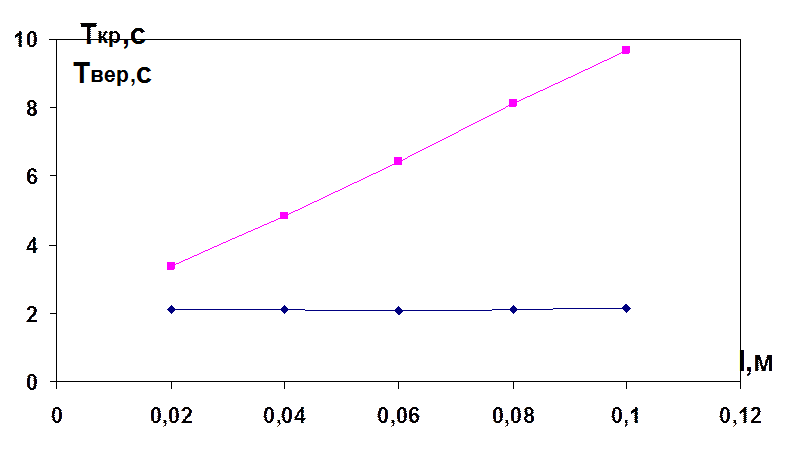
График зависимостей для случая жесткого закрепления:

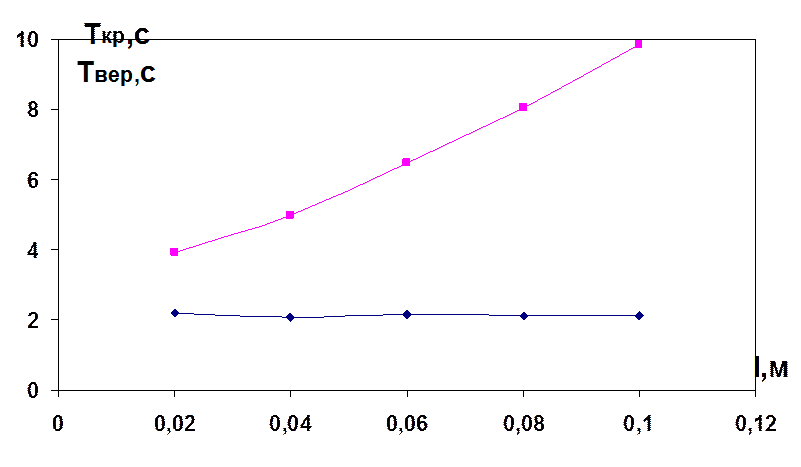
График зависимостей теоретических значений периода:

Вывод:

В процессе подготовки к работе и ее выполнения мы ознакомились и усвоили методику проведения эксперимента по определению периода колебаний и расчета момента инерции системы; уравнение движения системы с двумя степенями свободы; получили представление о механизме взаимного перехода вертикальных и крутильных колебаний пружинного маятника; применять теорию погрешностей для обработки результатов прямого и косвенного измерений. В результате эксперимента мы обнаружили, что характер закрепления маятника заметно влияет только на величину периода крутильных колебаний и почти не влияет на вертикальные.

1 2

Скачать файл