










Теоретическая часть
В механике очень давно исследуется движение пружинного маятника. Простота конструкции и обилие физических явлений, сопровождающих его движение, позволяет использовать этот маятник для многих целей. Но не все физические эффекты, сопровождающие его движение, широко представлены в учебной литературе. Например, одним из таких явлений можно назвать возникновение крутильных колебаний у маятника, реализованного на основе витой пружины. Как нам известно, лишь недавно в курсе общей физики МГУ появилось обсуждение механизмов, приводящих к возникновению этих интересных крутильных и вертикальных колебаний пружинного маятника.
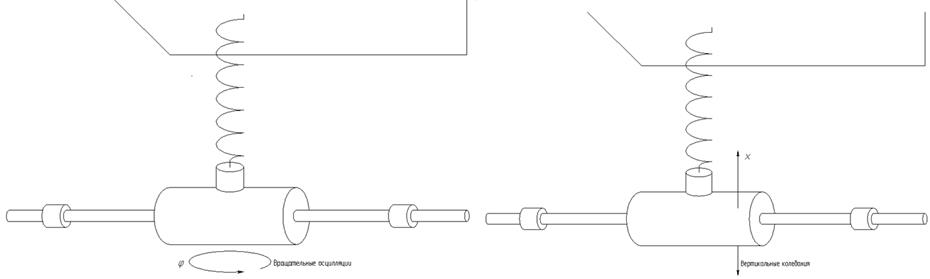
возникновению этих интересных
крутильных и вертикальных колебаний пружинного маятника.
Рис. 1
Для исследования свойств маятника воспользуемся методом Лагранжа, для чего запишем уравнения Лагранжа:
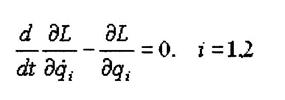
(1)
Здесь q1=x - вертикальная координата груза, отсчитываемая от положения равновесия (удлинение пружины), q2=φ - угловая координата закручивания груза вокруг вертикальной оси (закручивание торцов пружины), L=T-U - функция Лагранжа, Т - кинетическая энергия и U- потенциальная энергия системы.
Для записи уравнений движения изучаемой системы необходимо знать кинетическую и потенциальную энергию маятника в явном виде.
Кинетическая энергия изображенной на рис. 1 системы равна:
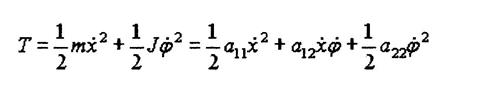
(2)
где m - масса груза, J - момент инерции груза относительно вертикальной оси, а11, а12, а22 - коэффициенты инерции системы.
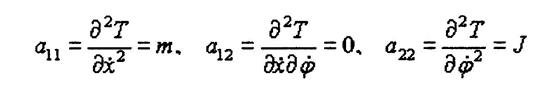
Нулевое значение коэффициента а и свидетельствует о том, что связь между колебаниями по различным координатам через коэффициенты инерции отсутствует.
Перейдем к нахождению потенциальной энергии маятника в произвольном положении. Нас интересует потенциальная энергия пружины в деформированном состоянии. Примем, что потенциальная энергия пружины в положении равновесия равна нулю.
Пусть пружинный маятник реализован на основе витой пружины с малым углом подъема витков и отношение диаметра проволоки к диаметру навивки гораздо меньше единицы. Пружина может испытывать два вида деформаций: продольную деформацию растяжения - сжатия, и угловую - закручивания витков относительно вертикальной оси (х и φ на рис. 1).
При этом проволока, из которой навита пружина, будет испытывать три вида деформаций: растяжения - сжатия, кручения и изгиба.
Примем за положительные те удлинения, которые увеличивают длину пружины, и те углы закручивания, которые закручивают пружину по ходу навивки.
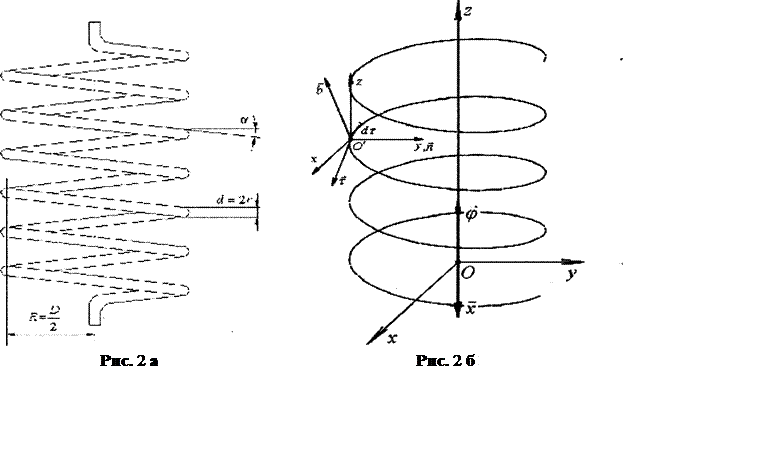
Ввиду малости получаемых пружиной деформаций параметры пружины изменяются незначительно, поэтому R и α будем считать постоянными (рис. 2.а.).
Если пружина деформирована по обеим координатам, то по условиям круговой симметрии все поперечные сечения витков равноправны. Для исследования достаточно рассмотреть любой элемент dτ любого витка.
Ось проволоки пружины располагается на винтовой линии. Для ее описания достаточно двух независимых параметров: среднего радиуса пружины R и угла подъема α винтовой линии.
Винтовая линия является пространственной кривой, поэтому для исследования пружины удобно использовать подвижную естественную систему координат. Ее начало отсчета располагается в исследуемой точке кривой, а оси направляются: по касательной к искомой кривой в сторону возрастания дуги от рассматриваемой точки (единичный вектор - орт τ), по главной нормали к кривой в рассматриваемой точке к центру кривизны (орт n), по бинормали к кривой в рассматриваемой точке (орт b).
Рассмотрим пружину в исходном недеформированном состоянии (рис. 2). Если система выводится из равновесия и имеет текущие координаты х и φ, то пружина получит соответствующие деформации, которые удобно изобразить векторами (рис. 2 б).
 |
Рассмотрим случай, когда витки пружины плоские, что соответствует α≈0.Тогда трехгранники О'хУz и О'τnb совпадают.
Это возможно, если витки плотно прилегают друг к другу, и r << R, где r - радиус проволоки пружины, a R - радиус навивки. Исходное состояние показано на рис. 3 а.
 |
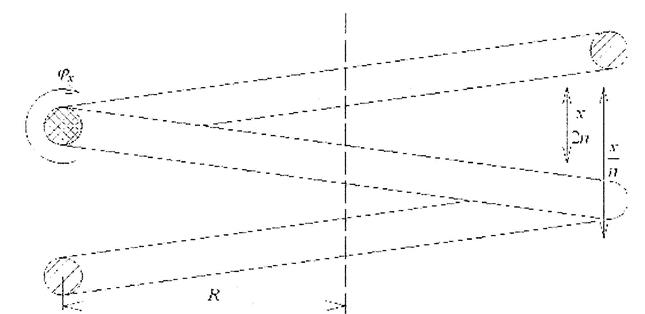
Рис. 3 б. Возникновение относительных углов закручивания
Исследуем, как изменится деформированное состояние элемента dτ, если пружину растянуть на величину χ (найдем влияние этой координаты на напряженное состояние проволоки отдельно от влияния координаты φ). Деформация всей пружины будет состоять из деформаций отдельных витков, а деформация витка - из деформаций отдельных половин витков (рис. 3 б). На каждую половину витка приходится х/2п от всей деформации, где п -количество витков рассматриваемой пружины (рис. 3 б). Если при деформации половины витка деформировался бы только один выделенный элемент витка dτ, сечение которого заштриховано квадратиками, то это была бы деформация кручения, а угол закручивания φх равнялся бы: φх=х/2пR. Но все элементы витка равноправны, и поэтому будут испытывать одинаковые деформации: dφx/dτ=x/2nRl, где l - длина проволоки половины витка.
Деформация dφx/dτ называется относительным углом закручивания, т.е. это тот угол, на который закручиваются два соседних сечения проволоки, отстоящие друг от друга на расстоянии dτ.
Аналогичная ситуация возникает, если исследовать влияние на деформированное состояние проволоки только координаты φ. Отличие будет только в том, что относительные утлы будут не закручивания, а изгиба.
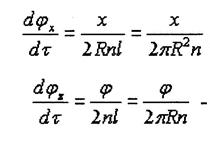 Найдем относительные
углы закручивания и изгиба элемента dτ:
Найдем относительные
углы закручивания и изгиба элемента dτ:
- деформация кручения; (3)
- деформация изгиба. (4)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.