Исследование свойств пружинного маятника, страница 2

Где х и φ – удлинение и угол закручивания все пружины, n – число витков, l=πR – длина проволоки половины витка.

Теперь перейдем к случаю, когда угол α мал. Трехгранники O'xyz и О'τпb  теперь не совпадают, и для нахождения углов закручивания нужно сделать соответствующий переход от одной системы координат к другой. Это сделать очень просто, т.к. оси О'у и О'п совпадают. Оси О'х и О'τ, а также оси O'z и О'b повернуты друг относительно друга на угол α (рис. 4).

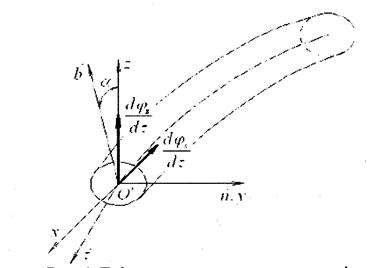Рис. 4. Деформации элемента проволоки dτ.

Потенциальная энергия пружины равна:

U=U_k+U_u                                     (5)

где U_k - потенциальная энергия кручения, U_u - потенциальная энергия изгиба. Выражения для U_k и U_u имеют вид :

 

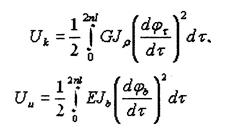
(6)

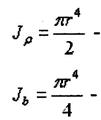где G - модуль упругости материала проволоки при сдвиге, Е - модуль упругости материала проволоки при растяжении,

полярный момент инерции сечения проволоки,

 осевой момент инерции сечения проволоки.

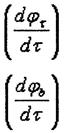- относительный угол закручивания,

- относительный угол изгиба.

Для расчета интегралов (6) необходимо найти относительные углы закручивания и изгиба. Выражения (3) и (4) не подходят, т.к. они записаны для системы координат O'xyz. Поэтому находим проекции векторов относительных углов закручивания на оси системы координат, связанной с проволокой – τ и b, по рис. 4 и рис. 5:

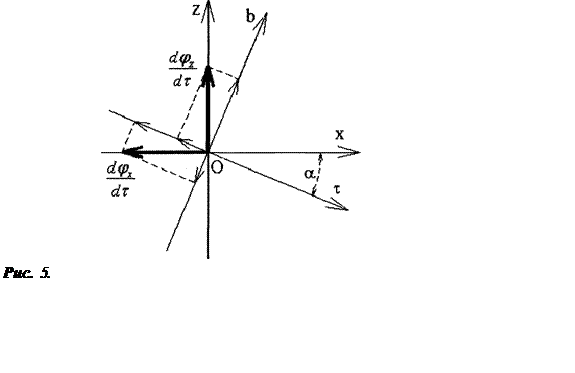(7)

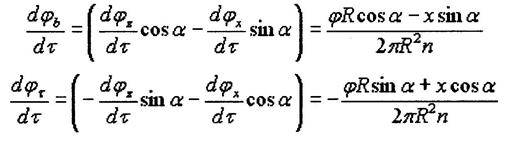
                                                                                                                       (8)

Подставим (7) и (8) в (6) и найдем потенциальную энергию: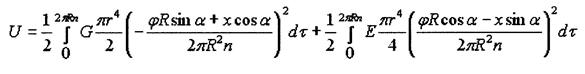  

(9)

Отсюда потенциальная энергия деформированной пружины равна:

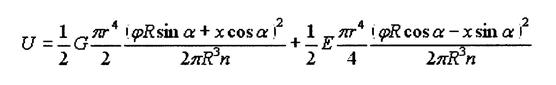(10)

Элементарные преобразования в (10) дают окончательное выражение для потенциальной энергии:

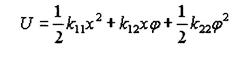                (11)

где к₁₁, к₁₂, к₂₂ - коэффициенты жесткости системы.

Коэффициент к₁₂ отличен от нуля, поэтому существует связь между колебаниями системы по координатам х и φ .

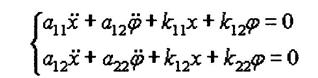Подставляя (2) и (11) в (1), получаем систему уравнений свободных колебаний маятника в общем виде:

(12)

В полученной системе (12) коэффициенты инерции и жесткости постоянные величины (не учтена зависимость R и α от х и φ) и в слагаемые не входят произведения координат. Поэтому система является линейной.

С помощью полученной системы (12) можно решить задачу нахождения закона движения маятника для заданных начальных условий или только найти частоты главных колебаний.

Предположим, что движение, описываемое уравнениями (12), является гармоническим, и будем искать частные решения системы в тригонометрической форме:

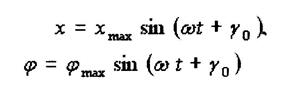
 (13)

где χ_мах, φ_мах, ω  и  γ₀ - постоянные величины.

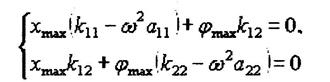Подставляя (13) в уравнения (12), придем к системе вида:

 (14)

Уравнения (14) являются линейными однородными уравнениями относительно χ_мах и φ_мах. Решение этих уравнений отлично от нуля, если определитель, составленный из коэффициентов при χ_мах, φ_мах, будет равен нулю:

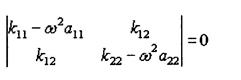 (15)

Соотношение (15) есть квадратное уравнение относительно ω2. Оно носит название характеристического уравнения или уравнения частот. Найдем с его помощью частоты колебаний:

Решение этого биквадратного уравнения известно:

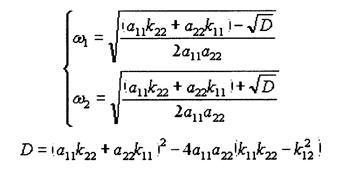 (16)

(17)

Частоты ω₁ и ω₂ найденные из (16) и (17) называются главными.

Частотам ω₁ и ω₂ соответствуют колебания вида (13). Таким образом, по каждой координате происходят колебания с амплитудами:  (верхний индекс показывает номер главного колебания, в котором берется амплитуда). Результирующее общее движение будет их суммой:

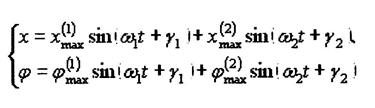
 (18)

Из системы (14) можно найти соотношения амплитуд и , а еще недостающие параметры, например , находятся из начальных условий для системы (12).

Рассмотрим случай свободных колебаний системы, когда частоты главных колебаний ω₁ и ω₂  очень мало отличаются друг от друга, то есть:

(19)

  Обозначим ξ - разность аргументов синусов в общем решении (18):

 (20)

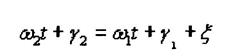При t=0 величина ξ(0)=γ₂-γ₁, а с возрастанием t эта разность из-за малости ω₁ - ω₂ увеличивается очень медленно. Тогда:

 (21)

Подставим это выражение в общее решение (18):

 

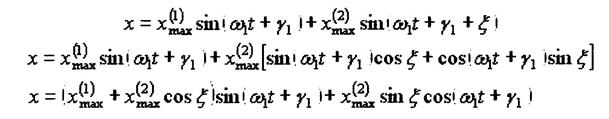
  (22)

Для другой координаты аналогично:

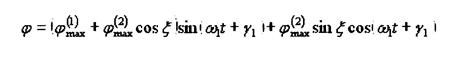 (23) 

Введем обозначения:

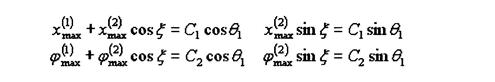 (24)

Тогда уравнения (18) после преобразований примут вид:

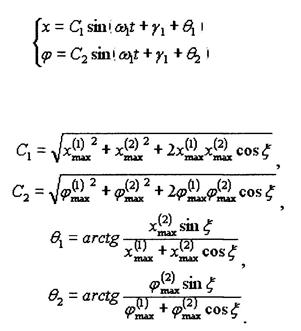 (25)

,где

Так как в выражениях для С₁, С₂, θ₁ и θ₂ входят sinξ и cosξ   а величина ξ  медленно изменяется с течением времени, то рассматриваемые колебания (18) не являются гармоническими. Период изменения амплитуд С₁, С₂, в этом случае значительно больше периода колебаний. Это явление и называется биениями.

Найдем соотношения параметров системы, при которых возникают биения. Явление биений возникает при выполнении условий (19). Можно записать для одной из частот, например ω₂, эквивалентное соотношению (19) условие:

 

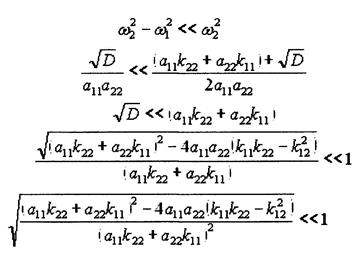
(26)

(27)

Возведем обе части выражения (27) в квадрат:

 

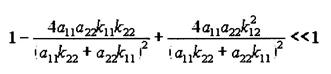
Отсюда следует, что:

(28)

Полученное неравенство (28) выражает необходимое условие существования биений. То есть выполнение этого условия не всегда приводит к появлению биений в движении системы.

Рассмотрим подробнее условие (19). Оно справедливо, если ω²₁≈ ω²₂. Найдем квадраты частот по выражениям (16) и (17) при выполнении условия (28):

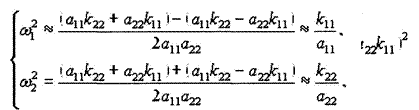Отсюда вытекает еще одно необходимое условие существования биений:

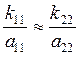     (29)

Оно требует выполнения определенного соотношения между параметрами системы. Условия (28) и (29) совместно определяют наличие биений.

Оценим условие (28) для малых углов α, при этом, очевидно, sinα≈α, sin²α≈α, cosα≈1, cos²α≈1:

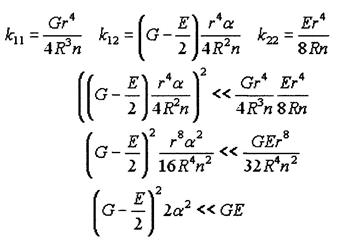 (30)

(31)

Неравенство (31) справедливо при малых углах α. Можно сделать вывод, что условие (28) также выполняется, когда пружина удовлетворяет уже упомянутым условиям: r << R, угол α мал. Поэтому определяющим будет соотношение (29).

Коэффициенты к₁₁ и к₂₂ из (30) совпадают с коэффициентами жесткости пружины.

Полученные выражения для коэффициентов инерции и жесткости дают возможность оценить величины собственных частот.