Исследование биений в колебательной системе с двумя степенями свободы на установке «маятник Уилберфорса», страница 2

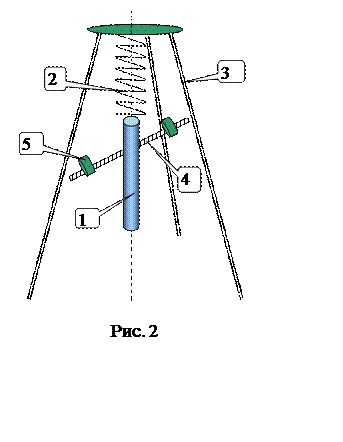
Устройство лабораторной установки показано на рис. 2. Металлический цилиндр 1 подвешен к пружине 2, верхний конец которой закреплён ни стойке 3. Цилиндр снабжён спицей 4 с перемещаемыми по ней гайками 5. Пружина обладает продольной (k) и крутильной (G) жесткостью, поэтому цилиндр может совершать как продольные, так и крутильные колебания.

Если отклонить цилиндр в вертикальном направлении без поворота вокруг своей оси, то на него будет действовать возвращающая сила

F = – kx.

В этом случае уравнение динамики поступательного движения

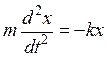
(m — полная масса цилиндра, включая спицу с дисками) можно привести к следующему уравнению гармонических колебаний:

,

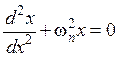где 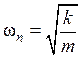                                                          (5)

— частота продольных колебаний.

Если повернуть цилиндр вокруг своей оси на некоторый угол φ без отклонения в вертикальном направлении, то на него будет действовать возвращающий момент силы относительно этой оси:

.

В этом случае уравнение динамики вращательного движения

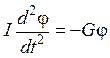
 (I — полный момент инерции цилиндра, включая спицу с гайками) можно привести к следующему уравнению гармонических колебаний:

,

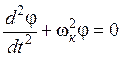где 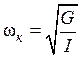                                                                                                                                     (6)

— частота крутильных колебаний.

В соответствии с формулами (5) и (6) периоды продольных и крутильных колебаний равны

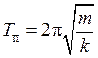 ,                                                                (7)

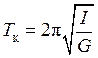.                                                               (8)

Величину T_к  можно регулировать, изменяя момент инерции тела I путем перемещения гаек 5 вдоль спицы 4, при этом период Т_п не изменяется, так как масса тела mостаётся постоянной.

Полный момент инерции цилиндра, включая спицу с гайками, равен

I= I₀ + 2m₀·l²,                                                             (9)

где I₀ — момент инерции цилиндра и спицы без гаек, m₀ — масса одной гайки, l — расстояние от оси цилиндра до гаек (предполагается, что гайки являются материальными точками и смещаются всегда симметрично относительно оси цилиндра).

Подстановка (9) в (8) приводит к следующей линейной зависимости  от l²:

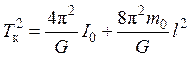.                                                    (10)

Это уравнение аналогично математической записи уравнения прямой линии .

Рассмотрим теперь условия, при которых в данной колебательной системе может наблюдаться режим биений. Пружина, применяемая в установке, обладает следующим свойством: при растяжении (или сжатии) её нижний конец слегка раскручивается (или закручивается) относительно верхнего закреплённого конца. Это приводит к тому, что продольные и крутильные колебания цилиндра оказываются хотя и слабо, но всегда связанными между собой. В результате такой связи продольные и крутильные колебания накладываются друг на друга — возникают суммарные колебания — так называемые биения с частотой .

В условиях, когда частоты ω_пиω_к близки друг другу, частота биений Δω оказывается достаточно низкой, а период биений значительно превышает величины T_пи T_к (рис. 3).

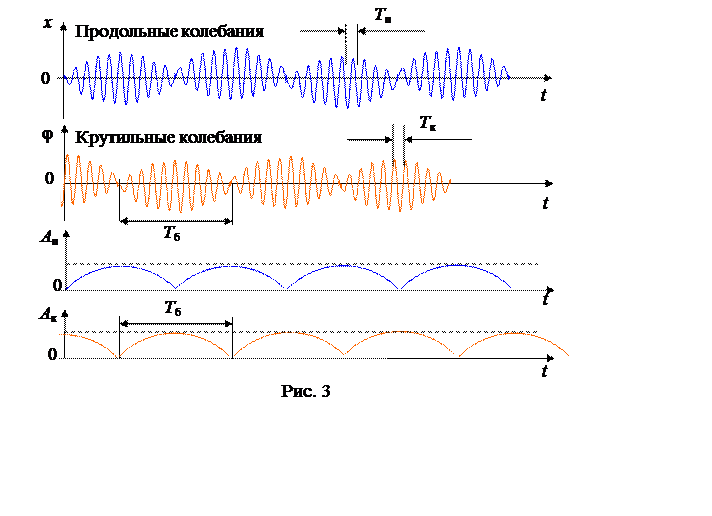
С энергетической точки зрения явление биений представляет собой периодическую перекачку энергии от одной степени свободы к другой, при этом максимум амплитуды продольных колебаний соответствует минимуму крутильных колебаний и наоборот.

За период биений принимают величину, равную промежутку времени между двумя ближайшими минимумами амплитуды, при этом

.

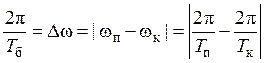Отсюда получаем следующую зависимость T_б от T_к:

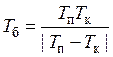.                                                     (11)

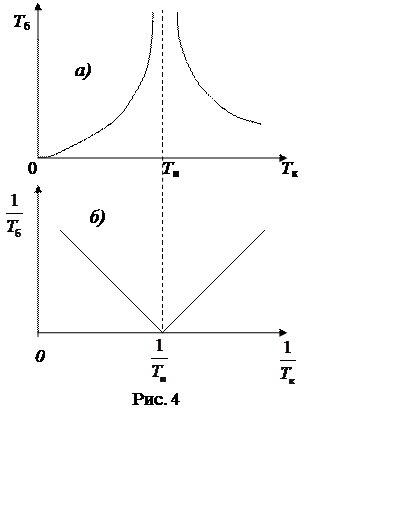Из графика этой зависимости (рис. 4а) видно, что при приближении T_к к T_п период биений резко возрастает.

Для экспериментальной проверки формулы (11) удобно представить ее в виде

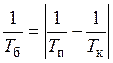.                  (12)

График зависимости 1/T_кот 1/T_пдолжен иметь вид двух отрезков прямых линий, сходящихся в точке на оси абсцисс, где периоды продольных и крутильных колебаний совпадают (1/T_к = 1/T_п). Угловые коэффициенты этих прямых должны быть равны (рис. 4б).

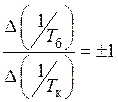.              (13)

7. Порядок выполнения работы

6.1. Определение периода продольных колебаний.

Скручивая гайки, установить их на спице симметрично, на максимальном удалении от оси цилиндра l_max. Отклонив цилиндр в вертикальном направлении, без поворота вокруг его оси, на расстояние порядка 2÷5 см, привести систему в состояние продольных (вертикальных) колебаний. Измерить по секундомеру полное время n= 20 периодов колебаний t_п1. Записать значение t_п1 в таблицу 1. Повторить измерения еще 3 раза с записью результатов t_п2иt_п3в таблицу 1.