ПРЕДИСЛОВИЕ
Данное учебное пособие, представляющее собой II часть
одного из основных разделов курса «Технология -и техника
добычи нефти», является продолжением конспекта лекций:
И. Т. Мищенко «Технология 'и техника добычи нефти. Теоретические основы подъема жидкости из скважин. Часть I». М., изд.МИНХйГП, 1977.
В учебном пособии изложен тот минимальный круг вопросов по теоретическим основам подъема жидкости из скважин, который является достаточным фундаментом для понимания и освоения .студентами «проблем и явлений, встречающихся в процессе эксплуатации скважин различным погружным оборудованием.
В пособии дан анализ классических исследований академика А. П. Крылова по движению газожидкостных смесей в вертикальных трубах и современных .методов расчета распределения давления в различных элементах скважины (лифт, участок «забой—дрием», затрубное пространство).
Рассмотрен ряд физических явлений, .протекающих в скважине, яредста-влено их математическое обоснование и практическое приложение. Основные методы расчета физических процессов, связанных с движением газожидкостных смесей, доведены до .алгоритмических программ.
1. ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ АКАДЕМИКА А. П. КРЫЛОВА
В 1934 ir. А. П. Крыловым были выполнены экспериментальные исследования движения воздухо-водяных смесей в вертикальных трубах на специальной установке, схема которой представлена на рис. 1.
Установка состоит из вертикальной трубы 1 диаметром dи длиной 18—20 ,м, воспроизводящей элементарный (подъемник, систем додачи .воды и воздуха, устройства 5 для измене-йяя .противодавлбнмя, отсекателей потока 2, пр'ием,ной си'сте-1й^ 9 и .комплекса контрольно-измерительных лриборов.
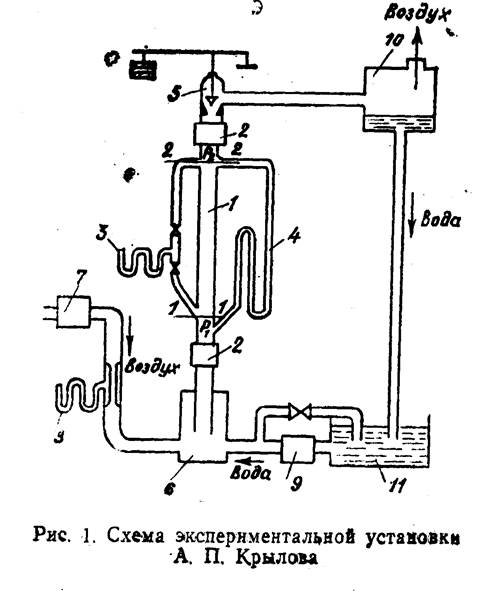
Эта установка позволяет:
1) изучать движение смеси по трубам различного диаметра;
2) воспроизводить реальные подъемники значительной длины;
3) замерять фактическую плотность движущейся смеси;
4) осуществлять процесс движения газожидкостной смеси с постоянным расходом жидкости q.^ и газа V независимо от .противодавления Рч;
5) производить точные зам'еры давлений Р, и ?з или АР в процессе установившегося движения газожидкостной смеси между сечениями 1—1 и 2—2.
Воспроизведение реальных подъемников значительной длины осуществлялось с помощью .регулировочного устройства 5: при изучении каждого последующего элементарного •подъемника давление Рч в нем устанавливалось равным давлению Pi в (Предыдущем элементарном подъемнике.
Методичеаки исследование проводилось следующим образом. Для экспериментальной трубы заданного диаметра d устанавливали определенный режим движения смеси: q ж== = const и V = const. Расход воздуха от .поршневого компрессора 7 замеряли измерителем расхода газа 8, а расход воды от поршневого .насоса 9—ооъемньш способо.м в емкости It. При установившемся движении воздухо-водяиой смеси давления Pi и ?2 (АР) определяли .манометром 3. Затем с помощью быстродействующшх отсекателей потока 2 отсекался объем воздухо-водя.ной смеси. После разделения смеси дифференциальным манометром 4 измеряли перепад давлении столба жидкости и газа в статических услов.иях. Затем движение смеси возобновлялось (после открытия отсекателей 2), давление Рч в сечении 2—2 с помощью устройства 5 устанавливалось равным давлению Pi в предыдущем случае и ци<кл повторялся.
Экспериментальные исследования проведены на трубах
диаметром Г/з^ 21/2// и 4".
Результаты экспериментальных исследований обрабатывали с целью получения следующих зависимостей:
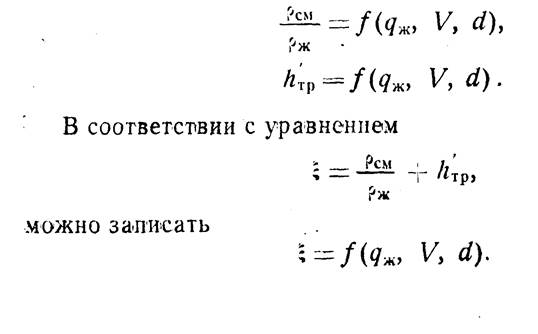
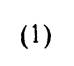
С целью получения основных. заяисимосФей, х-арактеризу-ющих работу .подъемника, А. П. Крыловым .проведена обработка полученного экспериментального материала в следующей последовательности.
Строились зависимости скорости газа v^ от суммарного расхода фаз (дж+ V) для разлйчньвх диаметров, .(подъемников. При этом были использованы и экспериментальные дан-яые Мура: .и Уайлда (та&ожидкостные смеси с различными <р:и-эичесжи'м;и Ьвойствамя). Эти зависимости представлены се-м'ёйством прямых, общим уравнением 'которого является
Зависимость слраведлива для диаметров подъемников Л", 1 W, 2", 242", У и 4" при суммарном расходе фаз от 60 до б^Тм^суг.' - , • .
Пренебрегая (плотностью газа по 'сравнению с плотностью
жидкости и смеси, из выражения йк» =• -Ssa-zl!. поаучают:
;;, . / ' ' ' . • ./' '?ж—?[ , '•
^аКй^таётем соотиошевий
имеем:
::',.{;•!'. "•-'-^••i1.!. ti :^" '•-.'-••: .... - • • ГМ- •" J "t
Подставляя выражение Vy из (2) в :<4), находят:
Таким образом, выражение (5) — это градиент гидростатического давления'с учетом относительной окаройти.
Для определения градиента потерь на трение h'rp == = if (<7ж, У, ri) с учетом граничныхусловий. движения смези экйперимеятальные данные обрабатывались в координатах:
Для яодъемйикпв с диаметрами Л", Г/з" и З^з" указанные экспериментальные зависимости .представляют собой оемей-ство -прямых, общим уравнением которого является
г^пля воды:" - ' '"'- ^ .'"^^." ""' """ :для-жидкб.сти-БяШстью 5 оП: -
Первое'слагаемое зависимости (6). выражает -градиент потерь на трение при движении, воздухо-водяной смеси, второе—градиент потерь на т.рение при движении чистого га.з'1 0,0094
(рассчитан с использияаяисм у"^-'"""» "——-^
• . , V d третье—•градиент .потерь на трение .при движении чистой воды (рассчитай с использованием формулы Блазиусз
0,3164 ':. . ^ =d i~==~ ). . ^ • У Re ^ ' • • : •
Подставляя 'выражения (4) и (5) •в уравнение (1), получаем:
V8
Уравнение (7) является уравнением движения смеси в элементарном (подъемнике •и справедливо для четочной структуры движения газожидк&стной смеси, поскольку все экспериментальные исследования проведены А. П. Крыловым имен-нп .лля этой структуры.
Проанализируем уравнение (7).
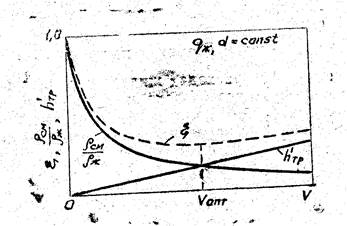
А. Рассмотрим влияние расхода газа V на P£M , ^тр' и ^ при
рж постоянном расходе жидкости д^л диаметре подъемника d. Графическая зависимость указаяньвх шара.метрав от расхода
газа V представлена на рис. 2: по мере роста V слагаемое-^1
рж снижается, а слагаемое h\p—увеличивается. Суммарный градиент потерь S имеет минимальное значение при 'некотором значении V = Уопт » т. е. пр,и достоянном расходе жидкости через подъемник постояниото диаметра d существует режим. суммарный градиент потерь «при котором минимален. Объемный расход газа V при этом режиме буд«м называть оптимальным (Vom)' ..-«йв»^
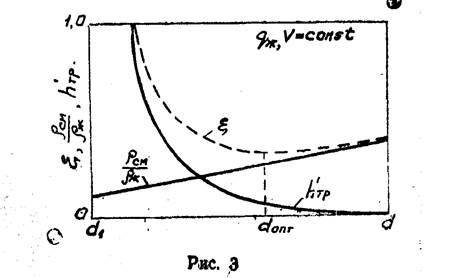
Б. Рассмотрим влияние диаметра подъем.ника с? на P£M ,
Рж
Лтр и § дри постоянных расходах жидкости q-м и газа V. Графическая зависимость представлена на рис. 3: при постоянном расходе смеси (<7ж Т- V) = const минимальный
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.