













Первая математическая
модель фильтрации жидкости через естественные пористые грунты была предложена
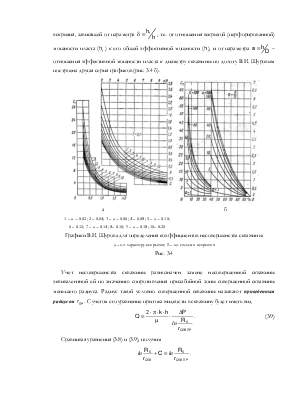
французским инженером Дарси в 1856 г., который в результате экспериментов (рис.
3.1) установил, что для не слишком высоких скоростей фильтрации объемный расход
![]() капельной жидкости в единицу времени,
приходящийся на единицу площади
капельной жидкости в единицу времени,
приходящийся на единицу площади ![]() поперечного сечения
потока, при плоскопараллельном течении прямо пропорционален потере напора
поперечного сечения
потока, при плоскопараллельном течении прямо пропорционален потере напора ![]() и обратно пропорционален длине фильтра
и обратно пропорционален длине фильтра ![]() . Здесь
. Здесь ![]() и
и ![]() ,
, ![]() и
и ![]() – первоначальные и конечные значения напора
и длины фильтра
– первоначальные и конечные значения напора
и длины фильтра
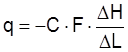 ,
(3.1)
,
(3.1)
где
![]() – коэффициент пропорциональности
(коэффициент фильтрации). Знаком минус учитывается направление течения в
сторону меньших значений давлений.
– коэффициент пропорциональности
(коэффициент фильтрации). Знаком минус учитывается направление течения в
сторону меньших значений давлений.
Соотношение (3.1) получило название закона фильтрации Дарси.
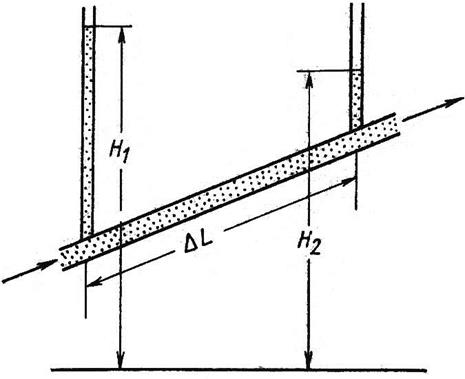
Схема проведения опытов Дарси
Рис. 3.1
Если левую и правую
части формулы (3.1) разделить на ![]() , то получим новое
выражение закона Дарси для скорости фильтрации жидкости через пористую среду
, то получим новое
выражение закона Дарси для скорости фильтрации жидкости через пористую среду
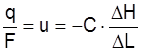 .
(3.2)
.
(3.2)
Скорость фильтрации ![]() , среднестатистическая скорость
, среднестатистическая скорость ![]() движения частиц жидкости по поровым
каналам и пористость
движения частиц жидкости по поровым
каналам и пористость ![]() связаны зависимостью:
связаны зависимостью:
![]() .
.
Коэффициент фильтрации ![]() , учитывающий свойства гидродинамической
системы «пористая среда – фильтрующаяся жидкость», естественно, зависит как от
параметров, характеризующих среду, так и от свойств жидкости. С учетом
коэффициента проницаемости
, учитывающий свойства гидродинамической
системы «пористая среда – фильтрующаяся жидкость», естественно, зависит как от
параметров, характеризующих среду, так и от свойств жидкости. С учетом
коэффициента проницаемости ![]() уравнение (3.2) примет
вид
уравнение (3.2) примет
вид
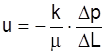 .
(3.3)
.
(3.3)
Исследования показали,
что линейный закон Дарси справедлив для не слишком высоких скоростей
фильтрации. Специальные исследования многих экспериментаторов позволили
предложить, по аналогии с трубной гидравликой, числа Рейнольдса для
характеристики потока: если число Рейнольдса (![]() ) меньше
критического (
) меньше
критического (![]() ), поток ламинарный, удовлетворяющий
линейному закону; если
), поток ламинарный, удовлетворяющий
линейному закону; если ![]() , фильтрация не подчиняется
линейному закону. Различные авторы по-разному определяли число Рейнольдса, в
соответствии с чем получали неодинаковые критические его значения. В.Н.
Щелкачевым была предложена следующая формула определения числа Рейнольдса
, фильтрация не подчиняется
линейному закону. Различные авторы по-разному определяли число Рейнольдса, в
соответствии с чем получали неодинаковые критические его значения. В.Н.
Щелкачевым была предложена следующая формула определения числа Рейнольдса
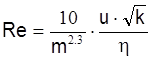 .
(3.4)
.
(3.4)
Критические значения чисел Рейнольдса по В.Н. Щелкачеву лежат в интервале:
![]() .
.
Зная значения пористости
![]() , проницаемости
, проницаемости ![]() пласта
и кинематической вязкости
пласта
и кинематической вязкости ![]() жидкости, можно вычислить
критическую скорость
жидкости, можно вычислить
критическую скорость ![]() фильтрации. В естественных условиях
превышение критической скорости фильтрации можно наблюдать только в небольшой
зоне пласта вблизи забоев скважин.
фильтрации. В естественных условиях
превышение критической скорости фильтрации можно наблюдать только в небольшой
зоне пласта вблизи забоев скважин.
В общем случае величина и направление скорости фильтрации жидкости являются функциями точки, и тогда удобно воспользоваться векторной формой записи закона Дарси
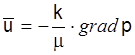 .
(3.5)
.
(3.5)
Правда, при этом необходимо учитывать, что пористая среда не является непрерывной средой, сколь угодно малые элементы которой отражают свойства среды в целом. Очевидно, твердые и жидкие фазы пористой среды не отражают свойства друг друга. Однако если каждой точке приписать свойства некоторой ее окрестности, достаточно большой по сравнению с размерами пор и достаточно малой по сравнению
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.