



2.5. Оценка конечной нефтеотдачи по материалам статистической
обработки промысловых данных
(пример)
2.5.1. Оценка конечной нефтеотдачи по темпам
снижения добычи нефти
Для оценки конечной нефтеотдачи используется график зависимости темпов снижения отбора нефти от текущего коэффициента нефтеизвлечения, представленный на рис. 2.1. Расчет охватывает период с ...... г. по ...... г., когда залежь находилась в поздней стадии разработки.
Экстраполируя фактическую кривую 1 до пересечения с осью абсцисс, можно определить величину конечной нефтеотдачи.
Для осуществления экстраполирования необходимо фактическую кривую 1 сгладить согласно уравнению, по которому она изменяется.
![]() Одним из способов корреляции по некоторой группе точек на плоскости ХY является метод наименьших квадратов
(МНК). В основе метода лежит следующее утверждение: наилучшая линия, проходя
через множество точек, рассеянных на плоскости XY, должна занимать положение, при котором сумма квадратов
отклонений от наиболее точного отсчета оказывается минимальной:
Одним из способов корреляции по некоторой группе точек на плоскости ХY является метод наименьших квадратов
(МНК). В основе метода лежит следующее утверждение: наилучшая линия, проходя
через множество точек, рассеянных на плоскости XY, должна занимать положение, при котором сумма квадратов
отклонений от наиболее точного отсчета оказывается минимальной:
, (2.1)
где Хс - точный, или истинный, отсчет; Х1, Х2, ..., Хn - совокупность отсчетов.
Фактическая зависимость t(hтек) наилучшим образом описывается уравнением вида:
t = аhтек + в. (2.2)
Неизвестные коэффициенты а и в определяются из системы уравнений:
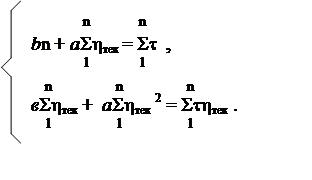
(2.3)
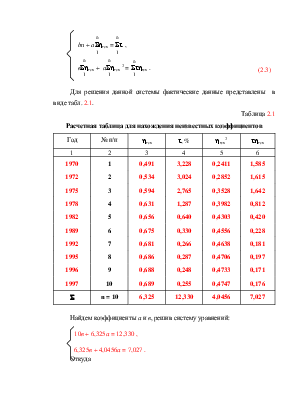
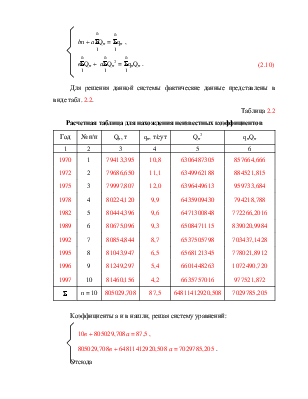
Для решения данной системы фактические данные представлены в виде табл. 2.1.
Таблица 2.1
Расчетная таблица для нахождения неизвестных коэффициентов
|
Год |
№ п/п |
hтек |
t, % |
hтек2 |
thтек |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1970 |
1 |
0,491 |
3,228 |
0,2411 |
1,585 |
|
1972 |
2 |
0,534 |
3,024 |
0,2852 |
1,615 |
|
1975 |
3 |
0,594 |
2,765 |
0,3528 |
1,642 |
|
1978 |
4 |
0,631 |
1,287 |
0,3982 |
0,812 |
|
1982 |
5 |
0,656 |
0,640 |
0,4303 |
0,420 |
|
1989 |
6 |
0,675 |
0,330 |
0,4556 |
0,228 |
|
1992 |
7 |
0,681 |
0,266 |
0,4638 |
0,181 |
|
1995 |
8 |
0,686 |
0,287 |
0,4706 |
0,197 |
|
1996 |
9 |
0,688 |
0,248 |
0,4733 |
0,171 |
|
1997 |
10 |
0,689 |
0,255 |
0,4747 |
0,176 |
|
S |
n = 10 |
6,325 |
12,330 |
4,0456 |
7,027 |
Найдем коэффициенты а и в, решив систему уравнений:
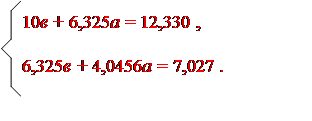 |
Откуда
а = - 17,149,
в = 12,080.
Подставив найденные значения в уравнение (2.2), построили прямую, которая наилучшим образом сглаживает фактическую зависимость t(hтек):
t = -17,149hтек + 12,080.
На рис. 2.1 ей соответствует теоретическая кривая 2.
Величина конечной нефтеотдачи, определяемая по точке пересечения линии 2 с осью абсцисс, составляет 0,704.
Точность корреляционной зависимости между параметрами t и hтек оценивается по коэффициенту корреляции. В случае линейной связи между исследуемыми параметрами коэффициент корреляции рассчитывается по формуле:
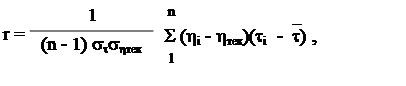 |
(2.4)
где`t и`h - математические ожидания, определяемые по формулам:
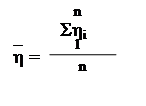
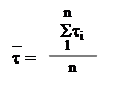 ; , (2.5), (2.6)
; , (2.5), (2.6)
st2, sh2 - дисперсии, вычисляемые по формулам
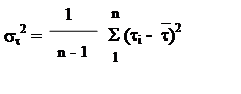 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.