Методы кажущегося сопротивления. Связь между кажущимся и истинным сопротивлением среды (по Дахнову), страница 2

      А(М)           Пусть в однородной  среде  с  УЭС  -  находится  точечный  источник  тока  А,создающий  ток  I.  В точке  М, удаленной  на  расстоянии  АМ от  заземления  А, потенциал:

                             

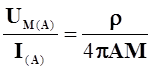
Поместим    источник  тока  в   точку  М,     а    в точке  А  будем  определять  потенциал  поля:

                           

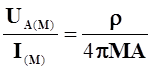
Т.к.      АМ=МА, то        (*)

Поскольку  УЭС  пропорционально  отношению  U/I, а коэффициент  зонда

()  определяется  только  взаимным  расположением  электродов и   не зависит  от их  назначения, равенство  (*)  и  является  доказательством  справедливости принципа взаимности. Принцип  взаимности  имеет  большое  практическое  значение:

  для  реализациии  разнообразных  типов  и  размеров  зондов,

  для  выбора  оптимальной  схемы  зонда,при  которой  минимальны  помехи.

Cхема  с двумя  измерительными  электродами  в  скважине  предпочтительнее, т.к.  при    ней  устраняются  индукционные  наводки  в  измерительных  жилах  кабеля  при  определениии разности  потенциалов.

Связь между  кажущимся  и  истинным  сопротивлением  среды

(  по  Дахнову  )

Кажущееся  сопротивление  среды    , измеренное  ПЗ в точке   М  Неоднородной  среды, отличается от его  истинного значения во столько  раз, во сколько потенциал  в этой точке   превышает  потенциал  однородной  среды   c  удельным  сопротивлением  :

                                           .

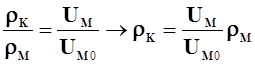  Выражая    потенциал   через  плотность   тока,           

имеем 

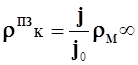                      ,  где     -  плотности  тока  в неоднородной  и  однородной средах ,  - среднее сопротивление среды в  интервале  Связь    ,       измеренного    градиент-зондом,      с   истинным     удельным сопротивлением среды  устанавливается  на  основе  формул:

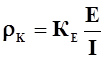       (1)             (2),  где   - истинное  УЭС  среды  между  электродами  М и N;     (3).

Подставив  в  (1)  выражение  (2)  и  (3)  получим

                                 

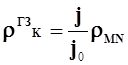
Из  формул  для        и      следует:

1)  кажущиеся  сопротивления, измеренные  ПЗ  и  ГЗ, пропорциональны   истинному  УЭС, в которой  находятся   измерительные  элементы;

2)  величина  КС  изменяется  пропорционально  плотности  тока  между  измерительными  элементами;

3)  при  перенесении  поверхности  раздела  сред  ПЗ-ом  величина  КС  изменяется  плавно( как  “реастатом” изменяется   ) , при  пересечении  ГЗ-ом  КС  изменяется скачком(  как   )  (отношение    в обеих  средах  приблизительно  одинаковы).

Формулы для     и      и следствия  из них позволяют на качественном  уровне  объяснить   форму  кривых     ПЗ  и  ГЗ    при    пересечении  границы  раздела (рис.   ).

Прямая  задача  КС  для  горизонтальной  границы  раздела

Связь  между кажущимся  и  истиннымсопротивлением  (по  Томсону)

Решается  применением  метода  зеркальных  изображений  Т о м с о н а, позволяющего  свести  кусочно-однородную  среду  к  однородной  и  воспользоваться  уравнением  .

                                   Суть метода  Томсона  в том,что деформация  линий тока

                                   при  приближении   к   оверхности  раздела  объясняется               

                                   о т р а ж е н и е м.  Поэтому потенгциал в нижней среде 1

                                   с     такой,   как   если   бы   кроме     фактического