Дискретная математика: Учебное пособие. Часть 4 - Основы математической логики

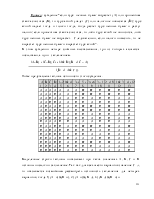
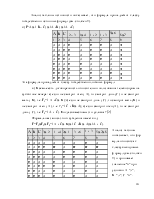
проекции коммутативна с операцией выбора;

·  r’=(r₁><r₂)= (r₂><r₁) - операция соединения коммутативна;

·  r’=(r₁><r₂)><r₃=r₁><(r₂><r₃) – операция соединения ассоциативна.

4.3.2 Реляционное исчисление

Если реляционная алгебра показывает способы исполне­ния различных операций над отношениями, то реляционное исчисление позволяет формировать новые отношения, исследуя значение логической функции на множестве кортежей отношения. Результатом алгебраической операции над отношениями является также отношение, которому может быть присвоено имя и которое имеет такой же статус, как и исходные отношения. В противоположность этому реляционное исчисление позволяет формулировать, например, арифметические запросы к атрибутам кортежей. В результате определения истинного значения логической функции формируется множество кортежей, которое не может быть поименовано и является промежуточным результатом для формирования нового отношения.

Пусть r’={ t’| F(t’)}, где t’ – кортеж отношения, а F(t) - формула логической функции.

Также как в исчислении предикатов введем понятия переменные и постоянные кортежи. Для обозначения перемен­ных кортежей используем символы x, y, z,... , а для постоянных кортежей - a, b, c,...Любой постоянный или переменный кортеж называют термом и обозначают t_i.

Элементарная формула определяется следующими правилами:

·  если r - имя отношения, а t - терм, то r(t) –элементарная формула;

·  если x и y – переменные кортежи и задан оператор сравнения двух или нескольких атрибутов A_i и A_j, то x(A_i)qy(A_j) - элементарная формула;                 

·  никаких других формул нет.

Также как в исчислении предикатов введем понятия “свободных“ и “связных” переменных-кортежей. Переменная-кортеж является связанным, если ему предшествует квантор по этой же переменной и свободным в противном случае.

          Формулы реляционного исчисления с переменными-кортежами могут быть определены из элементарных формул рекурсивно:

·  любая элементарная формула есть формула, т.е. F= r(t) и F= x(A_i)qy(A_j);

·  если F₁ и F₂ -формулы, то (ùF₁), (F₁Ú F₂), (F₁& F₂) также формулы;

·  если x - переменный кортеж, F(x) - формула, то $_x(F)  и "_x(F) также формулы.

·  никаких иных формул, кроме построенных по 1), 2), и 3) нет.

Итак, r’={ t’| F(t) }   есть множество свободных переменных-кортежей в F(t), формируемое связанными переменными-кортежами для истинного значения формулы F(t).

Операцию выборки на языке реляционного исчисления с переменными-кортежами записывают так:

r’={t’| $_x(r(x)&(x(A_i)qk_di))} или r’={t’| $_x(r(x)&(x(A_i)qx(A_j)))}.

Квантор существования используют потому, что накладываемые условия (x(A_i)qk_di) или (x(A_i)qx(A_j)) формируют частное суждение на множестве кортежей отношения. Условия могут быть  заданы функциями k_di:=f(A_i) или A_j:=f(A_i, A_j).

Операцию проекции на языке реляционного исчисления с переменными-кортежами записывают так:

r’={t’| "_x(r(x)&(t’[1]=x(A_i))&(t’[2]=x(A_j))&..&(t’[n]=x(A_n))}.

Квантор всеобщности используют потому, что в результирующем отношении используют все кортежи исходного отношения.

Операцию объединения на языке реляционного исчисления с переменными-кортежами записывают так:

r’={t’| "_x "_y(r₁(x)&r₂(y)&((t’=x)Ú(t’=y))}.

Квантор всеобщности используют потому, что в новое отношение следует перенести все кортежи отношений r₁(x) и r₂(y).

Операцию разности на языке реляционного исчисления с переменными-кортежами записывают так:

r’={t’| $_x$_y(r₁(x)&r₂(y)&((t’=x)&ù(t’=y))}.

Кванторы существования используют потому, что накладываются условия для извлечения только таких кортежей первого отношения, которых нет во втором.

Операцию пересечения на языке реляционного исчисления с переменными-кортежами записывают так:

r’={t’| $_x$_y(r₁(x)&r₂(y)&(t’=x)&(t’=y)}.

Кванторы существования используют потому, что должны быть одинаковые кортежи в первом и втором отношениях.

Операцию прямого произведения на языке реляционного исчисления с переменными-кортежами записывают так:

r’={t’|$_x$_y(r₁(x)&r₂(y)&(t’[1]=x[1])&(t’[2]=x[2])..&(t’[n₁]=x[n₁])&

(t’[n₁+1]=y[1]) &(t’[n₁+2]=y[2]).. &(t’[n₁+n₂]=y[n₂]))}.

Кванторы существования используют потому, что каждый кортеж второго