матрице (17) выделим независимые нули, построив цепочку (подчеркнутые нули). Работник А закреплен за работой 2, В — за работой IV) С — за работой III, D — за работой I. Оценка Смах = 7 + 13 + 14 + 10 = 44 [2,c.252-256].
Вывод: задачи о назначении ставятся, в основном, как задачи линейного и дискретного программирования. И то и другое предполагает задание целевой функции и ограничений в линейной форме. Задачи о назначении – это одна из особенностей в моделировании задач распределения разных типов.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Вариант 8. Задача 1. Решить симплекс-методом:
Канонический вид:
Max z=X1+X2 Max z=X1+X2+0X3+0X4
3X1+2X2
5
3X1+2X2+X3=5
X22
X2+X4=2
Xi
0;
|
Cj |
БП |
1 |
1 |
0 |
0 |
Bi |
|
X1 |
X2 |
X3 |
X4 |
|||
|
0 |
X3 |
3 |
2 * |
1 |
0 |
5 |
|
0 |
X4 |
0 |
1 ** |
0 |
1 |
2 * |
|
Z |
-1 |
-1 * |
0 |
0 |
0 |
|
|
Cj |
БП |
1 |
1 |
0 |
0 |
Bi |
|
X1 |
X2 |
X3 |
X4 |
|||
|
0 |
X3 |
3 |
0 |
1 |
0 |
1 |
|
1 |
X2 |
0 |
1 |
0 |
1 |
2 |
|
Z |
-1 |
0 |
1 |
1 |
2 |
|
|
Cj |
БП |
1 |
1 |
0 |
0 |
Bi |
|
X1 |
X2 |
X3 |
X4 |
|||
|
1 |
X1 |
1 |
0 |
0,33 |
0 |
0,33 |
|
1 |
X2 |
0 |
1 |
0 |
1 |
2 |
|
Z |
0 |
0 |
1,33 |
1 |
2,33 |
|
* - ключевые столбец и строка
** - ключевое число
Ответ: X1=0,33; X2=2; Z(X)=2,33
Задача 2. Решить симплекс-методом:
Канонический вид:
Min z=X1+X2 Min z=X1+X2 Min z=X1+X2+0X3+0X4
3X1+2X25
-3X1-2X2-5 -3X1-2X2+X3=-5
X22 -X2 -2 -X2+X4=-2
Xi0;
|
Cj |
БП |
1 |
1 |
0 |
0 |
Bi |
|
X1 |
X2 |
X3 |
X4 |
|||
|
0 |
X3 |
-3 ** |
-2 |
1 |
0 |
-5 * |
|
0 |
X4 |
0 * |
-1 |
0 |
1 |
-2 |
|
Z |
-1 * |
-1 |
0 |
0 |
0 |
|
|
Cj |
БП |
1 |
1 |
0 |
0 |
Bi |
|
X1 |
X2 |
X3 |
X4 |
|||
|
1 |
X1 |
1 |
0,67 |
0,33 |
0 |
1,67 |
|
0 |
X4 |
0 |
-1 |
-1 |
1 |
-2 |
|
Z |
0 |
-0,33 |
-0,67 |
0 |
1,67 |
|
|
Cj |
БП |
1 |
1 |
0 |
0 |
Bi |
|
X1 |
X2 |
X3 |
X4 |
|||
|
1 |
X1 |
1 |
0 |
-0,34 |
0,67 |
0,33 |
|
1 |
X2 |
0 |
1 |
1 |
-1 |
2 |
|
Z |
0 |
0 |
-0,34 |
-0,33 |
2,33 |
|
* - ключевые столбец и строка
** - ключевое число
Ответ: X1=0,33; X2=2; Z(X)=2,33
Задача 3. Решить симплекс-методом с искусственным базисом:
Канонический вид:
MaxZ=7X1+2X2+3X3 MaxZ=7X1+2X2+3X3+0S1+0S2+0S3+0S4
7X1+2X2+3X318
7X1+2X2+3X3+S1=18
4X1+3X210
4X1+3X2+S2=10
2X1+3X2+X39 2X1+3X2+X3-S3=9
X1+X2+X35 X1+X2+X3-S4=5
X10
M – задача:
MaxZ=7X1+2X2+3X3+0S1+0S2+0S3+0S4-MR1-MR2
7X1+2X2+3X3+S1=18
4X1+3X2+S2=10
2X1+3X2+X3-S3+R1=9
X1+X2+X3-S4+R2=5 Таблица 1
|
Cj |
БП |
7 |
2 |
3 |
0 |
0 |
0 |
0 |
-M |
-M |
Bi |
|
X1 |
X2 |
X3 |
S1 |
S2 |
S3 |
S4 |
R1 |
R2 |
|||
|
0 |
S1 |
7 |
2 * |
3 |
1 |
0 |
0 |
0 |
0 |
0 |
18 |
|
0 |
S2 |
4 |
3 * |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
10 |
|
-M |
R1 |
2 |
3 ** |
1 |
0 |
0 |
-1 |
0 |
1 |
0 |
9 * |
|
-M |
R2 |
1 |
1 * |
1 |
0 |
0 |
0 |
-1 |
0 |
1 |
5 |
|
Z |
-7 |
-2 * |
-3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
-3M |
-4M * |
-2M |
0 |
0 |
M |
M |
0 |
0 |
-14M |
||
Таблица 2
|
Cj |
БП |
7 |
2 |
3 |
0 |
0 |
0 |
0 |
-M |
Bi |
|
|
X1 |
X2 |
X3 |
S1 |
S2 |
S3 |
S4 |
R2 |
||||
|
0 |
S1 |
5,67 |
0 |
2,33 * |
1 |
0 |
0,67 |
0 |
0 |
12 |
|
|
0 |
S2 |
2 |
0 |
-1 * |
0 |
1 |
1 |
0 |
0 |
1 |
|
|
2 |
X2 |
0,67 |
1 |
0,33 * |
0 |
0 |
-0,33 |
0 |
0 |
3 |
|
|
-M |
R2 |
0,33 |
0 |
0,67 ** |
0 |
0 |
0,33 |
-1 |
1 |
2 * |
|
|
Z |
-5,67 |
0 |
-2,33 * |
0 |
0 |
-0,67 |
0 |
0 |
6 |
||
|
-0,33M |
0 |
-0,67M |
0 |
0 |
-- -0,33M |
M |
0 |
-2M |
|||
Таблица 3
|
Cj |
БП |
7 |
2 |
3 |
0 |
0 |
0 |
0 |
Bi |
|
X1 |
X2 |
X3 |
S1 |
S2 |
S3 |
S4 |
|||
|
0 |
S1 |
4,52 * |
0 |
0 |
1 |
0 |
-0,48 |
3,48 |
5,04 |
|
0 |
S2 |
2,49 * |
0 |
0 |
0 |
1 |
1,49 |
-1,49 |
3,99 |
|
2 |
X2 |
0,51** |
1 |
0 |
0 |
0 |
-0,49 |
0,49 |
2,01 * |
|
3 |
X3 |
0,49 * |
0 |
1 |
0 |
0 |
0,49 |
-1,49 |
2,99 |
|
Z |
-4,52 * |
0 |
0 |
0 |
0 |
-0,48 |
-3,48 |
12,96 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
Таблица 4
|
Cj |
БП |
7 |
3 |
0 |
0 |
0 |
0 |
Bi |
|
X1 |
X3 |
S1 |
S2 |
S3 |
S4 |
|||
|
0 |
S1 |
0 |
0 |
1 |
0 |
3,86** |
-0,86 |
-12,77 * |
|
0 |
S2 |
0 |
0 |
0 |
1 |
3,88 * |
-3,88 |
-5,82 |
|
7 |
X1 |
1 |
0 |
0 |
0 |
-0,96 * |
0,96 |
3,94 |
|
3 |
X3 |
0 |
1 |
0 |
0 |
0,96 * |
-1,96 |
1,06 |
|
Z |
0 |
0 |
0 |
0 |
-4,82 * |
0,86 |
30,77 |
|
Таблица 5
|
Cj |
БП |
7 |
3 |
0 |
0 |
0 |
Bi |
|
X1 |
X3 |
S1 |
S3 |
S4 |
|||
|
0 |
S3 |
0 |
0 |
0 |
1 |
-0,22 ** |
-3,31* |
|
0 |
S2 |
0 |
0 |
1 |
0 |
-3,02 * |
7,02 |
|
7 |
X1 |
1 |
0 |
0 |
0 |
0,75 * |
0,76 |
|
3 |
X3 |
0 |
1 |
0 |
0 |
-1,75 * |
4,24 |
|
Z |
0 |
0 |
0 |
0 |
-0,21 * |
14,82 |
|
Таблица 6
|
Cj |
БП |
7 |
3 |
0 |
0 |
Bi |
|
X1 |
X3 |
S1 |
S4 |
|||
|
0 |
S4 |
0 |
0 |
0 |
1 |
15,05 |
|
0 |
S2 |
0 |
0 |
1 |
0 |
52,46 |
|
7 |
X1 |
1 |
0 |
0 |
0 |
-10,52 |
|
3 |
X3 |
0 |
1 |
0 |
0 |
30,57 |
|
Z |
0 |
0 |
0 |
0 |
18,07 |
|
* - ключевые столбец и строка
** - ключевое числo
Ответ: X1= -10,52; X3=30,57 ; Z(X)=18,07
Задача 4. Решить симплекс-методом с искусственным базисом:
Канонический вид:
Min z=6X1+5X2+X3 Min z=6X1+5X2+X3+0S1+0S2+0S3
7X1+2X2+4X321 7X1+2X2+4X3+S1 =21
5X1+3X2+X315 5X1+3X2+X3+S2=15
3X1+X2+4X39 3X1+X2+4X3-S3=9
M – задача:
Min z=6X1+5X2+X3+0S1+0S2+0S3 +MR1
7X1+2X2+4X3+S1 =21
5X1+3X2+X3+S2=15
3X1+X2+4X3-S3+R1=9 Таблица 1
|
Cj |
БП |
6 |
5 |
1 |
0 |
0 |
0 |
M |
Bi |
|
X1 |
X2 |
X3 |
S1 |
S2 |
S3 |
R1 |
|||
|
0 |
S1 |
7 |
2 |
4 * |
1 |
0 |
0 |
0 |
21 |
|
0 |
S2 |
5 |
3 |
1 * |
0 |
1 |
0 |
0 |
15 |
|
M |
R1 |
3 |
1 |
4 ** |
0 |
0 |
-1 |
1 |
9 * |
|
Z |
-6 |
-5 |
-1 * |
0 |
0 |
0 |
0 |
0 |
|
|
3M |
M |
4M * |
0 |
0 |
-M |
0 |
9M |
||
Таблица 2
|
Cj |
БП |
6 |
5 |
1 |
0 |
0 |
0 |
Bi |
|
X1 |
X2 |
X3 |
S1 |
S2 |
S3 |
|||
|
0 |
S1 |
4 * |
1 |
0 |
1 |
0 |
1 |
12 |
|
0 |
S2 |
4,25 * |
2,75 |
0 |
0 |
1 |
0,25 |
12,75 |
|
1 |
X3 |
0,75** |
0,25 |
1 |
0 |
0 |
-0,25 |
2,25 * |
|
Z |
-5,25* |
-4,75 |
0 |
0 |
0 |
-0,25 |
2,25 |
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
Таблица 3
|
Cj |
БП |
6 |
5 |
0 |
0 |
0 |
Bi |
|
X1 |
X2 |
S1 |
S2 |
S3 |
|||
|
0 |
S1 |
0 |
-0,33 |
1 |
0 |
2,33 |
0 |
|
0 |
S2 |
0 |
1,33 |
0 |
1 |
1,67 |
0 |
|
1 |
X1 |
1 |
0,33 |
0 |
0 |
-0,33 |
3 |
|
Z |
0 |
-3 |
0 |
0 |
-2 |
18 |
|
Задача 6.
Для производства 4 видов продукции затрачивается 3 вида ресурсов А, В, С. Затраты ресурсов на 1-цу продукции – в таблице. Известно, что от реализации 1-го вида продукции предприятие получает прибыль 3 рубля, 2-го – 4, 3-го – 3, 4-го – 1 рубль. Определить какие виды продукции предприятие должно производить и в каком объёме, чтобы получить максимум дохода, если предприятие затрачивает ресурса А – 12 единиц, В – 8 единиц, С – 48 единиц.
|
Ресурсы |
Продукция |
Затраты |
|||
|
1 |
2 |
3 |
4 |
||
|
А |
3 |
- |
2 |
1 |
12единиц |
|
В |
1 |
2 |
- |
4 |
8 единиц |
|
С |
3 |
5 |
4 |
2 |
48единиц |
|
Прибыль |
3 рубля |
4 рубля |
3 рубля |
1 рубль |
- |
Виды продукции – х
Прибыль от 1-го вида продукции составит 3Х1, прибыль от 2-го вида продукции составит 4Х2, прибыль от 3-го вида продукции составит 3Х3, прибыль от 4-го вида продукции составит 1Х4. Эта величина должна быть максимизирована.
Max Z=3X1+4X2+3X3+X4
Если затраты ресурса А на 1 - го вида продукцию составляет 3 единицы, 3 – го - 2 единицы, 4 – го – 1 единицу, то сопоставляя общие затраты ресурса А с наличными ресурсами можно записать следующее:
3X1+2X3+X412
Аналогично записываем ограничения и для 2 – х других ресурсов:
X1+2X2+4X48
3X1+5X2+4X3+2X448
Переменные Х не могут быть отрицательными по смыслу, значит:
X10; X20; X30;
X40
Таким образом, описанную выше экономическую ситуацию, можно записать в виде следующей модели линейного программирования в развернутом виде:
Найти X1, X2, X3, X40 максимизирующие функции 3X1+4X2+3X3+X4= Z, при ограничениях:
3X1+2X3+X412
X1+2X2+4X48
3X1+5X2+4X3+2X448
Cокращенная форма модели:
Xj - количество продукции j-ro вида, где j = 1 ...n;
Pj - прибыль от реализации продукции j-ro вида;
Аij - нормы затрат сырья i-ro вида на единицу продукции j-ro вида;
S i - запасы сырья i-ro вида (i = 1.. .m).
Тогда математическая модель задачи распределения запишется следующим образом:
Z=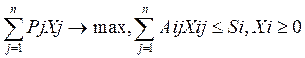
Задача 7.
В смесь должно входить не менее 12 единиц вещества А, 21 единицы вещества В и 32 единицы вещества С. Вещества содержатся в 3-х продуктах в следующих пропорциях: в 1-ом продукте вещества А – 1 единица, вещества В – 3 единицы и вещества С – 4 единицы; во 2-ом продукте, соответственно, 1 – 2 – 3 и в 3-ем продукте – 2 – 1 – 2 . B каком количестве должны входить продукты в смесь, чтобы стоимость её была минимальной, если учесть, что весовая единица 1-го продукта стоит 20 рублей, 2-го – 20 рублей, 3-го – 10 рублей.
|
Вещества |
Продукты |
Состав |
||
|
1 |
2 |
3 |
||
|
А |
1 |
1 |
2 |
12 единиц |
|
В |
3 |
2 |
1 |
21 единица |
|
С |
4 |
3 |
2 |
32 единицы |
|
Стоимость |
20рублей |
20рублей |
10 рублей |
|
Продукты – Х, стоимость стремится к минимуму.
Тогда функция цели может быть записана так:
Z= 20X1+20X2+10X3 
min
Ограничения по содержанию необходимых веществ:
X1+X2+2X312 - по
веществу А
3X1+2X2+X321 - по веществу B
4X1+3X2+2X332 - по веществу C
Ограничения Xi0
В общем виде математическую модель задачи о смесях можно записать следующим образом:
Z=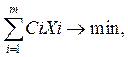
при ограничениях:
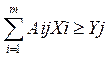- ограничения на
содержание необходимых веществ
Aij - содержание j-ro вещества в единице i-ro продукта;
Yj - необходимое содержание j-ro вещества в продукте.
Транспортная задача.
В 3-х пунктах отправления (на складах) находится соответственно 100,80,120т горючего. В пункты назначения требуется доставить соответственно 60,140,100т горючего. Стоимость перевозки тонны горючего из пункта а1 в пункты b1, b2, b3 соответственно 4,5,1 ден. ед., из пункта а2 – 6,3,4 ден. ед., а из пункта а3 – 3,2,4 ден. ед. Составить оптимальный план перевозок горючего так, чтобы общая сумма транспортных расходов была оптимальной.
Исходный опорный план
Определение первоначального допустимого плана методом ”северо-западного угла”. Таблица 1
|
b1 |
b2 |
b3 |
b4 |
ai |
|
|
a1 |
50 1 |
20 4 |
30 7 |
3 |
100 |
|
a2 |
7 |
6 |
80 8 |
9 |
80 |
|
a3 |
7 |
2 |
20 4 |
100 8 |
120 |
|
вj |
50 |
20 |
130 |
100 |
300 |
Таблица 2
|
b1=1 |
b2=4 |
b3=7 |
b4=11 |
ai |
|
|
a1=0 |
50 1 |
20 4 |
30 - 7 |
+ 3 |
100 |
|
a2=-1 |
7 |
6 |
80 8 |
9 |
80 |
|
a3=3 |
7 |
2 |
20 + 4 |
100 - 8 |
120 |
|
вj |
50 |
20 |
130 |
100 |
300 |
a1=0, а1+с11= b1=1, а1+с13= b3=7, b3- с33= а3= 3, а3+с34= b4= 11, b3- с23= а2= -1
а1+с12= b2=4
а1+с14 b4
0+3< 11 – не выполняется
а2+с21 b1
-1+7> 1 – выполняется
а2+с22 b2
-1+6> 4 - выполняется
а2+с24 b4
-1+9< 11 - не выполняется
а3+с31 b1
3+7> 1 - выполняется
а3+с32 b2
3+2> 4 - выполняется
Z=1860 Таблица 3
|
b1=1 |
b2=4 |
b3=-1 |
b4=3 |
ai |
|
|
a1=0 |
50 1 |
20 - 4 |
7 |
30 + 3 |
100 |
|
a2=-9 |
7 |
+ 6 |
80 - 8 |
9 |
80 |
|
a3=-5 |
7 |
2 |
50 + 4 |
70 - 8 |
120 |
|
вj |
50 |
20 |
130 |
100 |
300 |
a1=0, а1+с11= b1=1, а1+с12= b2=4, а1+с14= b4= 3, b4- с34= а3=-5, а3+с33= b3= -1,
b3- с23= а3=-9
а1+с13 b3
0+7> -1 – выполняется
а2+с21 b1
-9+7< 1 – не выполняется
а2+с22 b2
-9+6< 4 - не выполняется
а2+с24 b4
-9+9< 3 - не выполняется
а3+с31 b1
-5+7> 1 - выполняется
а3+с32 b2
-5+2< 4 - не выполняется
Z=1650 Таблица 4
|
b1=1 |
b2=-3 |
b3=-1 |
b4=3 |
ai |
|
|
a1=0 |
50 1 |
4 |
7 |
50 3 |
100 |
|
a2=-9 |
7 |
20 6 |
60 - 8 |
+ 9 |
80 |
|
a3=-5 |
7 |
2 |
70 + 4 |
50 - 8 |
120 |
|
вj |
50 |
20 |
130 |
100 |
300 |
a1=0, а1+с11= b1=1, а1+с14= b4=3, b4- с34= а3= -5, а3+с33= b3= -1, b3- с23= а2= -9
а2+с22= b2=-3
а1+с12 b2
0+4>-3 - выполняется
а1+с13 b3
0+7>-1 - выполняется
а2+с21 b1
-9+7<1 -не выполняется
а2+с24 b2
-9+9<3 - не выполняется
а3+с31 b1
-5+7>1 - выполняется
а3+с32 b2
-5+2=3 - выполняется
Z=1480 Таблица5
|
b1=1 |
b2=0 |
b3=2 |
b4=3 |
ai |
|
|
a1=0 |
50 1 |
4 |
7 |
50 3 |
100 |
|
a2=-6 |
7 |
20 6 |
10 8 |
50 9 |
80 |
|
a3=-2 |
7 |
2 |
120 4 |
8 |
120 |
|
вj |
50 |
20 |
130 |
100 |
300 |
a1=0,а1+с11=b1=1, b4- с24= а2= -6, а2+с22= b2=0, b2- с32=а3=-2, а2+с23=b3=2
а1+с14=b4=3,
а1+с12 b2
0+4>0 – выполняется
а1+с13 b3
0+7>2 – выполняется
а2+с21 b1
-6+7=1 - выполняется
а3+с31 b1
-2+7>1 - выполняется
а3+с32 b2
-2+2=0 - выполняется
а3+с34 b4
-2+8>3 - выполняется
Z=1330
Количество базисных клеток должно быть на единицу меньше суммарного количества поставщиков и потребителей вместе взятых(m+n-1) m=3;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
