Роль вычислительной техники в управлении. Комплекс технических средств автоматизированных систем управления строительством. Подсистема материального обеспечения

документы учитывают специфику строительных организаций и содержат рекомендации по выбору типа и расчета количества средств сбора, регистрации первичной обработки данных, средств подготовки, обработки и накопления информации; средств представления и отображения данных, включая видеотерминальные устройства, телекоммуникационных средств; средств диспетчеризации и устройств счета продукции, в том числе устройств автоматизации оперативного контроля за ходом производственного процесса, средств оргтехники, вспомогательного оборудования и материалов, комплектов проектной документации.

  При проектировании состава комплекса технических средств рекомендуется использовать типовые проектные решения (ТПР), которые включают в себя методические и проектные материалы на каждый элемент КТС, достаточные для разработки и привязки технической документации.

41. Подсистема материального обеспечения

Подсистема материально-технического обеспечения предназначена для повышения эффективности управления материально-техническим снабжением на производстве путем применения экономико-математических методов, вычислительной техники и организационно-технических мероприятий. В этой подсистеме выделяют следующие основные функции: планирование, оперативный учет и контроль, решение оптимизационных задач, анализ, регулирование, нормативные расчеты.

Подсистема материального обеспечения в составе автоматизированной системы управления обеспечивает:

1. Расчет потребности в материалах, комплектующих изделиях, аппаратуре и оборудовании:

— расчет годовой потребности в материалах, комплектующих изделиях, аппаратуре и оборудовании;

— расчет специфицированной потребности в материалах и комплектующих изделиях;
— составление заявок; уточнение и конкретизация потребности в материалах, комплектующих изделиях, аппаратуре и оборудовании.

2. Формирование планов материально-технического обеспечения и контроль их выполнения:

— формирование планов материально-технического обеспечения;
— учет и контроль реализации фондов;
— учет движения материалов;
— учет движения материалов и комплектующих изделий на складах;
— контроль уровней запасов материалов и комплектующих изделий;
— учет расхода материалов и комплектующих изделий по подразделениям и заказам.

3. Контроль обеспечения материалами и комплектующими изделиями на планируемый период.
4. Составление статистической отчетности.

Задача

Решением задачи является определение такого плана перевозки, при котором суммарная стоимость перевозок минимальна.

Для определения исходных данных нужно заполнить матрицу, где ai соответствует запасам продукта на пункте отправления, а bj – потребности в продукте на пункте получения.

Перенумерованными клетками матрицы моделируются пути между пунктами отправления и пунктами получения.

Исходные данные:

i)  а1=300; а2=350; а3=400; а4=200;

j) b1=39; b2=100; b3=41; b4=35; b5=35; b6=300;b7=200; b8=220; b9=280.

Проверяем выполнение условия ∑ ai = ∑ bj

∑ai=1250 = ∑bj=1250. Условие выполняется.

Таблица 1. Исходная матрица стоимостей

Таблица 2. Базисный план (метод двойного предпочтения)

Количество заполненных клеток должно быть равно суммарному количеству строк и столбцов без единицы.

m+n-1=4+9-1=12

Количество заполненных клеток n=11. Условие не выполняется, поэтому в одну из клеток подставляем 0 (клетка 1-1).

Целевая функция плана:

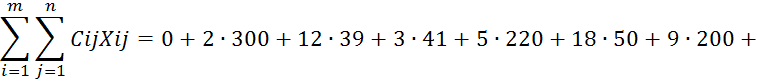
Таблица 3. Базисный план (метод северо-западного угла)

Количество заполненных клеток должно быть равно суммарному количеству строк и столбцов без единицы.

m+n-1=4+9-1=12

Количество заполненных клеток n=12. Условие выполняется.

Целевая функция плана:

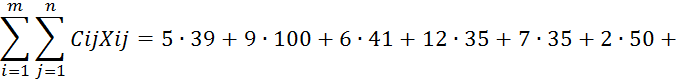
Таким образом, целевая функция плана, решенного методом двойного предпочтения, значительно экономичнее.

Далее рассматриваем план, решенный методом двойного предпочтения.

Для улучшения первоначального базисного плана применяем метод потенциалов.

Условия оптимальности плана:

для занятых клеток    - Vj-Ui = Cij

для свободных клеток  -  Vj-Ui ≤ Cij

Принимаем U2=0.

Таблица 4. Подбор потенциалов

Производим проверку условия для свободных клеток по формуле:

Vj-Ui ≤ Cij

Данные расчетов сводим в таблицу 5.

Таблица 5. Проверка условия для свободных клеток

Клетка 1,2

11-7=4<9 – условие выполняется

Клетка 2,2

11-0=1<13 и т.д.

Расчеты показали, что условие Vj-Ui ≤ Cij выполняется не для всех клеток.

Клетка 2,4

15-0=15>9 – условие не выполняется

Клетка 2,5

13-0=13>8 – условие не выполняется

Клетка 2,7

17-0=17>11 – условие не выполняется

Клетка 1,9

18-7=11>3 – условие не выполняется.

Следовательно, необходимо оптимизировать план. Выбираем клетку с максимальным нарушением  и строим от нее контур перераспределения.

Клетка 2,7

до перераспределения условные затраты составили:

после перераспределения условные затраты составили:

От остальных клеток построить контур перераспределения не представляется возможным.

Таблица 6. Оптимизированный план

Целевая функция плана:

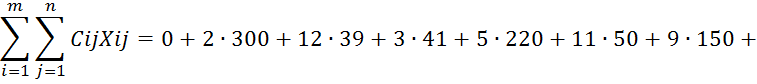
Вывод:  из сравнения двух вариантов базисных планов  (первоначальный и оптимизированный) видно, что второй более оптимальный, т. к. значение целевой функции для него меньше, значит второй план более экономичен. Экономический эффект выражается в величине достигнутой экономии