Из условия постановки только поперечных ребер жесткости, для обеспечения местной устойчивости стенки балки, толщина стенки составит:
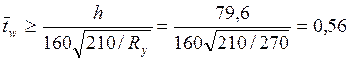 см
см
Принимаем толщину стенки равной t=10 мм по ГОСТ 19903-74
Определим оптимальную высоту стенки по формуле:
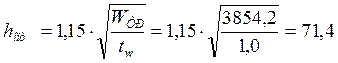 см
см
Сечение стенки по ГОСТ 19903-74 принято 800 х 10 мм.
Суммарную площадь сечения поясов определим по формуле:
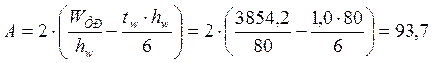 см2
см2
Площадь верхнего с учетом коэффициента β будет равно:
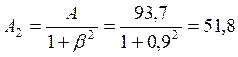 см2
см2
площадь нижнего будет равной: ![]() см2
см2
Ширину верхнего пояса назначают
из соотношения:![]() ,
,
получим 800/4 = 200 мм принимаем ширину верхнего пояса равной 200 мм.
Требуемая толщина пояса будет
равна: 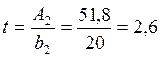 см
см
По ГОСТ 82-70 принимаем сечение верхнего пояса равным 200 х 28 мм.
Проверим устойчивость пояса:
![]() , получим:
, получим: ![]()
устойчивость пояса обеспечена.
Ширина нижнего пояса ![]() см.
см.
Размеры поясов (ГОСТ 82-70) приняты: верхнего – 200 х 28; нижнего – 180 х 28.
3.3 Проверочные расчеты сечения подкрановой балки
Определим геометрические характеристики сечения подкрановой балки:
-площадь поясов: ![]() см2
см2
![]() см2;
см2;
-площадь сечения подкрановой балки: ![]() см2
см2
Определим координату центра тяжести сечения балки:
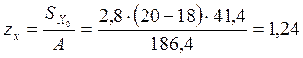 см
см
Моменты инерции относительно центральной оси брутто и нетто будут равны:
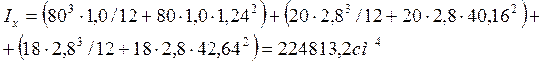
![]() см4
см4
![]() см4
см4
Моменты сопротивления для верхней и нижней точек сечения:
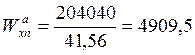 см3
см3 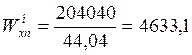 см3
см3
Статические моменты верхнего S2, нижнего S1поясов и полусечения S:
![]() см3
см3 ![]() см3
см3
![]() см3
см3
Геометрические характеристики тормозной балки:
Для швеллера №16: A=18,1см2; Ix=747см4; Iy=63,3см4; Wx=93,4см3. Лист тормозной балки толщиной 6мм.
Площадь сечения балки ![]() см2
см2
Координата центра тяжести: 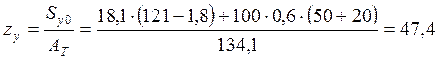 см
см
Момент инерции брутто и нетто:
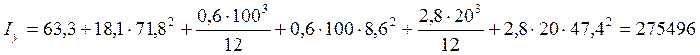 см4
см4
![]() см4
см4
![]() см4
см4
Моменты сопротивления для крайних точек тормозной балки:
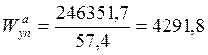 см3
см3 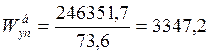 см3
см3
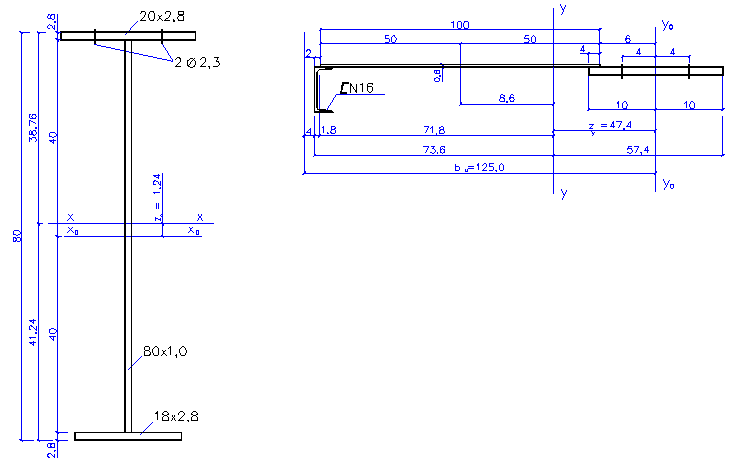 Рисунок
11 – Поперечные сечения подкрановой и тормозной балок
Рисунок
11 – Поперечные сечения подкрановой и тормозной балок
В сварных подкрановых балках проверяют наибольшие краевые напряжения общего изгиба и напряжения в стенке, обусловленные деформациями общего изгиба, а также местного смятия.
Максимальные напряжения общего изгиба – нормальное в середине балки определяют по формулам:
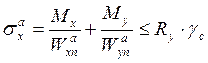
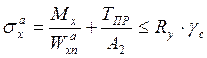 ,
получим:
,
получим:
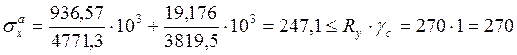 МПа
МПа
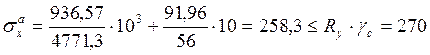 МПа
МПа
- напряжения в нижнем поясе вычисляются по формуле:
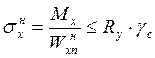 , получим
, получим 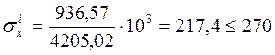 МПа
МПа
Запас прочности по нормальным
напряжениям общего изгиба допустимо, так как составляют ![]() .
.
Касательные напряжения на опоре подкрановой балки вычисляются по формуле:
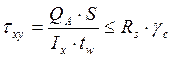 , получим:
, получим: 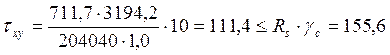 МПа
МПа
Для проверки прочности по местным напряжениям предварительно определим сумму собственных моментов инерции пояса и кранового рельса - I1f,
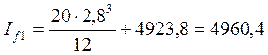 см4
см4
определим условную длину распределения местного давления по формуле:
![]() см
см
тогда 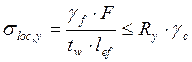 , получим
, получим 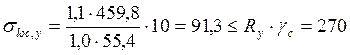 МПа
МПа
Для стенок балок должны так же выполнятся условия прочности
по приведенным и средним касательным напряжениям: ![]() , где
, где
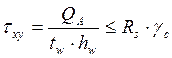 , получим:
, получим: 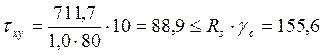 МПа
МПа
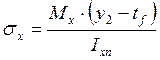 , получим
, получим 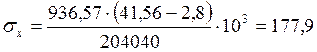 МПа
МПа
Вычислим прочность по приведенным напряжениям:
![]() МПа
МПа
Проверим прочность наружного пояса по формуле:
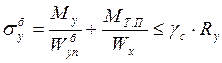 , получим
, получим 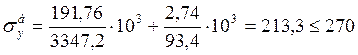 МПа
МПа
Жесткость подкрановой балки проверяем от нормативной
нагрузки ![]()
по формуле: 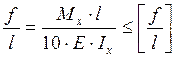
Вычислим момент от нормативной нагрузки: ![]() кН∙м, откуда
кН∙м, откуда
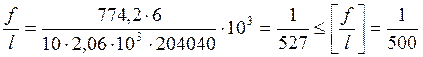
условие жесткости выполняется:
3.4 Проектирование деталей подкрановой балки
Для определения толщины верхних
поясных швов необходимо вычислить усилия T и V на опоре
балки: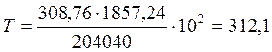 кН/м
кН/м 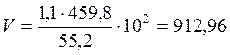 кН/м
кН/м
тогда по металлу шва: 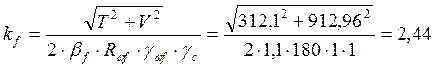 мм
мм
по металлу границы сплавления: 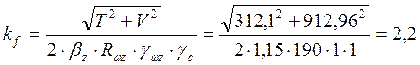 мм
мм
По таблице 38* СНиП II.23-81* принимаем катет шва равным 6 мм.
|
Опорное ребро балки выполняют с фрезерованным торцом и рассчитывают на смятие и устойчивость. Примем толщину ребра равной толщине пояса tf=22мм, ширину ребра определим из условия прочности на торцевое смятие от опорного давления:
|
Рисунок 12 – Сечение опорного ребра балки |
Принимаем b=200мм. Проверим устойчивость ребра, предварительно определив:
![]() см
см
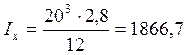 см4;
см4; ![]() см2;
см2;
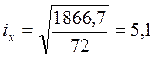 см
см 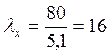 ,
откуда φ = 0,977 (поучено
интерполяцией).
,
откуда φ = 0,977 (поучено
интерполяцией).
В расчетную площадь включено ребро и устойчивая часть стенки
![]() см2.
см2.
Проверим условие устойчивости:
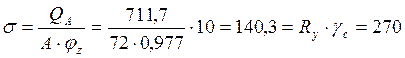 МПа
МПа
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.