



Задание №1.
a) Номинативная шкала, т.к. классификация происходит по названиям, у которых нет количественной или порядковой оценки. Тип измерений: качественное.
b) Порядковая шкала. Классифицирующие ячейки образуют последовательность по принципу меньше-больше, но не известно количественное выражение. Тип измерений: качественное-количественное.
c) Шкала равных отношений. Характеризует объекты пропорционально степени выраженности измеряемого свойства. Тип измерений: количественное.
d) Интервальная шкала. Каждое из возможных значений признака отстоит от другого на равном расстоянии. Тип измерений: количественное.
e) Порядковая шкала.
f) Интервальная шкала, если измерять время и Порядковая шкала, если измерять психологическое различие. Одна и та же разница во времени при быстром решении задачи, более значима для оценки психологического различия, чем при долгом. Следовательно нет равного расстояния. Тип измерений: количественное либо качественно-количественное.
Задание №2
Найти параметры распределения для следующих 75 чисел.
|
141 |
104 |
101 |
130 |
148 |
92 |
87 |
115 |
91 |
96 |
100 |
133 |
124 |
92 |
123 |
|
132 |
118 |
98 |
101 |
107 |
97 |
124 |
118 |
146 |
107 |
110 |
111 |
138 |
121 |
129 |
|
106 |
135 |
97 |
108 |
108 |
107 |
110 |
101 |
129 |
105 |
105 |
110 |
116 |
113 |
123 |
|
83 |
127 |
112 |
114 |
105 |
127 |
114 |
113 |
106 |
139 |
95 |
105 |
95 |
105 |
106 |
|
109 |
102 |
102 |
102 |
89 |
108 |
92 |
131 |
86 |
134 |
104 |
94 |
121 |
107 |
103 |
a) X =111
σ = 14,9 (корень из дисперсии)
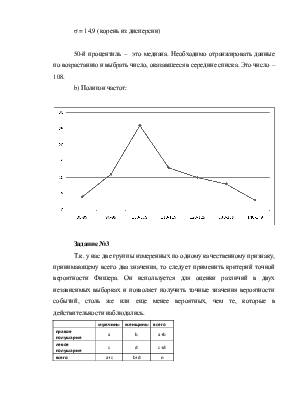
50-й процентиль – это медиана. Необходимо отранжировать данные по возрастанию и выбрать число, оказавшееся в середине списка. Это число – 108.
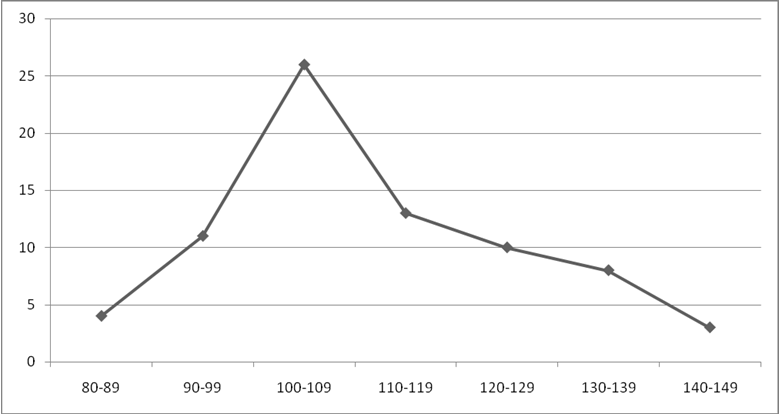
b) Полигон частот:
Задание №3
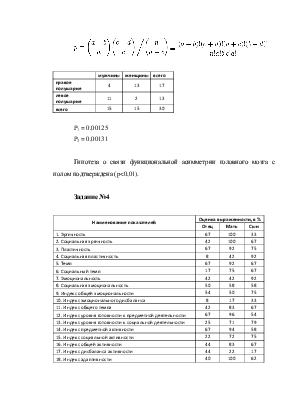
Т.к. у нас две группы измеренных по одному качественному признаку, принимающему всего два значения, то следует применить критерий точной вероятности Фишера. Он используется для оценки различий в двух независимых выборках и позволяет получить точные значения вероятности событий, столь же или еще менее вероятных, чем те, которые в действительности наблюдались.
|
мужчины |
женщины |
всего |
|
|
правое полушарие |
a |
b |
a+b |
|
левое полушарие |
c |
d |
c+d |
|
всего |
a+c |
b+d |
n |
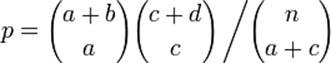
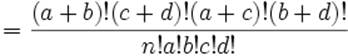
|
мужчины |
женщины |
всего |
|
|
правое полушарие |
4 |
13 |
17 |
|
левое полушарие |
11 |
2 |
13 |
|
всего |
15 |
15 |
30 |
P1 = 0,00125
P2 = 0,00131
Гипотеза о связи функциональной асимметрии головного мозга с полом подтверждена (p<0,01).
Задание №4
|
Наименование показателей |
Оценка выраженности, в % |
||
|
Отец |
Мать |
Сын |
|
|
1. Эргичность |
67 |
100 |
33 |
|
2. Социальная эргичность |
42 |
100 |
67 |
|
3. Пластичность |
67 |
92 |
75 |
|
4. Социальная пластичность |
8 |
42 |
92 |
|
5. Темп |
67 |
92 |
67 |
|
6. Социальный темп |
17 |
75 |
67 |
|
7. Эмоциональность |
42 |
42 |
92 |
|
8. Социальная эмоциональность |
50 |
58 |
58 |
|
9. Индекс общей эмоциональности |
54 |
50 |
75 |
|
10. Индекс эмоционального дисбаланса |
8 |
17 |
33 |
|
11. Индекс общего темпа |
42 |
83 |
67 |
|
12. Индекс уровня готовности к предметной деятельности |
67 |
96 |
54 |
|
13. Индекс уровня готовности к социальной деятельности |
25 |
71 |
79 |
|
14. Индекс предметной активности |
67 |
94 |
58 |
|
15. Индекс социальной активности |
22 |
72 |
75 |
|
16. Индекс общей активности |
44 |
83 |
67 |
|
17. Индекс дисбаланса активности |
44 |
22 |
17 |
|
18. Индекс адаптивности |
40 |
100 |
62 |
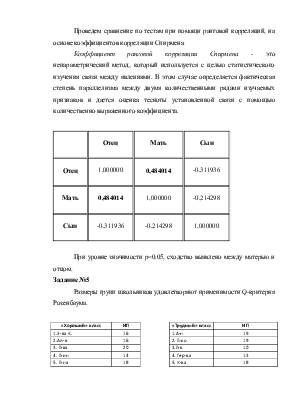
Проведем сравнение по тестам при помощи ранговой корреляций, на основе коэффициентов корреляции Спирмена.
Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
|
Отец |
Мать |
Сын |
|
|
Отец |
1,000000 |
0,484014 |
-0,311936 |
|
Мать |
0,484014 |
1,000000 |
-0,214298 |
|
Сын |
-0,311936 |
-0,214298 |
1,000000 |
При уровне значимости p=0.05, сходство выявлено между матерью и отцом.
Задание №5
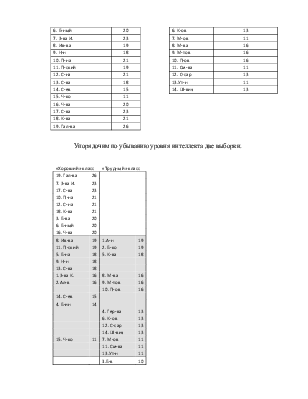
Размеры групп школьников удовлетворяют применимости Q-критерия Розенбаума.
|
«Хороший» класс |
ИП |
«Трудный» класс |
ИП |
|
|
1.3-ва К. |
16 |
1.A-н |
19 |
|
|
2.Ал-в |
16 |
2. Б-ко |
19 |
|
|
3. Б-ва |
20 |
З.Б-в |
10 |
|
|
4. Б-ин |
14 |
4. Гер-ва |
13 |
|
|
5. Б-на |
18 |
5. К-ва |
18 |
|
|
6. Б-ный |
20 |
6. К-ов |
13 |
|
|
7. 3-ва И. |
23 |
7. М-ов |
11 |
|
|
8. Ив-ва |
19 |
8. М-ва |
16 |
|
|
9. Н-н |
18 |
9. М-тов |
16 |
|
|
10. П-на |
21 |
10. П-ов |
16 |
|
|
11. П-ский |
19 |
11. См-ва |
11 |
|
|
12. С-на |
21 |
12. С-сар |
13 |
|
|
13. С-ва |
18 |
13.Ут-н |
11 |
|
|
14. С-ев |
15 |
14. Ш-вич |
13 |
|
|
15. Ч-ко |
11 |
|||
|
16. Ч-ва |
20 |
|||
|
17. С-ва |
23 |
|||
|
18. К-ва |
21 |
|||
|
19. Гал-ва |
26 |
|||
Упорядочим по убыванию уровня интеллекта две выборки.
|
«Хороший» класс |
«Трудный» класс |
||
|
19. Гал-ва |
26 |
||
|
7. 3-ва И. |
23 |
||
|
17. С-ва |
23 |
||
|
10. П-на |
21 |
||
|
12. С-на |
21 |
||
|
18. К-ва |
21 |
||
|
3. Б-ва |
20 |
||
|
6. Б-ный |
20 |
||
|
16. Ч-ва |
20 |
||
|
8. Ив-ва |
19 |
1.A-н |
19 |
|
11. П-ский |
19 |
2. Б-ко |
19 |
|
5. Б-на |
18 |
5. К-ва |
18 |
|
9. Н-н |
18 |
||
|
13. С-ва |
18 |
||
|
1.3-ва К. |
16 |
8. М-ва |
16 |
|
2.Ал-в |
16 |
9. М-тов |
16 |
|
10. П-ов |
16 |
||
|
14. С-ев |
15 |
||
|
4. Б-ин |
14 |
||
|
4. Гер-ва |
13 |
||
|
6. К-ов |
13 |
||
|
12. С-сар |
13 |
||
|
14. Ш-вич |
13 |
||
|
15. Ч-ко |
11 |
7. М-ов |
11 |
|
11. См-ва |
11 |
||
|
13.Ут-н |
11 |
||
|
З.Б-в |
10 |
||
Количество значений первого ряда, которые больше максимального значения второго ряда S1 = 9, количество значений второго ряда, которые меньше минимального значения первого S2=1
Q= S1 + S2 = 10
Из таблицы для размеров групп n1=19 и n2=14, QКРИТ = 9, при p≤0,01
Следовательно, принимается гипотеза о том, что уровень развития интеллекта у «Хорошего» класса выше, чем у «трудного» класса (p≤0,01).
Задание №6
Условие задания подходит для того, чтобы использовать T-критерий Вилкоксона.
|
№ |
До |
После |
Разность |
|
1 |
24 |
22 |
2 |
|
2 |
12 |
12 |
0 |
|
3 |
42 |
41 |
1 |
|
4 |
30 |
31 |
-1 |
|
5 |
40 |
32 |
8 |
|
6 |
55 |
44 |
11 |
|
7 |
50 |
50 |
0 |
|
8 |
52 |
32 |
20 |
|
9 |
50 |
32 |
18 |
|
10 |
22 |
21 |
1 |
|
11 |
33 |
34 |
-1 |
|
12 |
78 |
56 |
22 |
|
13 |
79 |
78 |
1 |
|
14 |
25 |
23 |
2 |
|
15 |
28 |
22 |
6 |
|
16 |
16 |
12 |
4 |
|
17 |
17 |
16 |
1 |
|
18 |
12 |
18 |
-6 |
|
19 |
25 |
25 |
0 |
Типичный сдвиг в сторону уменьшения количества ошибок. Следовательно, выдвигаемая гипотеза H1 состоит в том, что коррекционная работа, проводимая психологом, действительно ведет к тому, что интенсивность сдвигов в сторону улучшения грамотности превышает интенсивность сдвигов в сторону ее ухудшения.
|
№ |
До |
После |
Разность |
Модуль |
Ранг |
|
1 |
24 |
22 |
2 |
2 |
10,5 |
|
2 |
12 |
12 |
0 |
0 |
2 |
|
3 |
42 |
41 |
1 |
1 |
6,5 |
|
4 |
30 |
31 |
-1 |
1 |
6,5 |
|
5 |
40 |
32 |
8 |
8 |
15 |
|
6 |
55 |
44 |
11 |
11 |
16 |
|
7 |
50 |
50 |
0 |
0 |
2 |
|
8 |
52 |
32 |
20 |
20 |
18 |
|
9 |
50 |
32 |
18 |
18 |
17 |
|
10 |
22 |
21 |
1 |
1 |
6,5 |
|
11 |
33 |
34 |
-1 |
1 |
6,5 |
|
12 |
78 |
56 |
22 |
22 |
19 |
|
13 |
79 |
78 |
1 |
1 |
6,5 |
|
14 |
25 |
23 |
2 |
2 |
10,5 |
|
15 |
28 |
22 |
6 |
6 |
13,5 |
|
16 |
16 |
12 |
4 |
4 |
12 |
|
17 |
17 |
16 |
1 |
1 |
6,5 |
|
18 |
12 |
18 |
-6 |
6 |
13,5 |
|
19 |
25 |
25 |
0 |
0 |
2 |
|
Сумма: |
190 |
||||
Тэмп = 6,5+6,5+13,5 = 26,5
Исходя из таблицы с критическими значениями критерия T Вилкоксона при 19 испытуемых, типичный сдвиг является достоверно преобладающим (p≤0,01), если Tэмп < 37, что в нашем случае выполняется.
Стоит отметить, что про эффективность коррекционной работы можно будет говорить более определенно, лишь при наличии контрольной группы.
Задание №7
|
Параметры распределений оценок интеллекта |
Группа риска I (13 человек) |
Группа риска II (67 человек) |
Группа риска III (33 человека) |
|
|
IQ fluid |
X |
100 |
96 |
94 |
|
σх |
17 |
10 |
12 |
|
|
IQ verb |
X |
13 |
8 |
6 |
|
σx |
4 |
3 |
2 |
|
Принимая предположение о нормальности распределения значений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.