изучаемых показателей (выделяют типы) – это типический отбор.
Собственно-случайный отбор – дает лотерея и жеребьевка.
В тиражах (например, денежной лотереи) применяется бесповторный собственно-случайный отбор. Жеребьевка производится с помощью фишек (написанных фамилий). Здесь применяется бесповторный и повторный отбор.
Механический отбор: т.к. собственно-случайный отбор используют редко, то обычно применяют районированный механический отбор.
Теоретически средняя ошибка выборки при механическом отборе определяется по формуле:
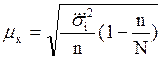 ,
,
где ![]() - средняя внутригрупповых дисперсий.
- средняя внутригрупповых дисперсий.
Когда имеем дело с неоднородными по изучаемым показателям совокупностями, в этом случае сначала осуществляем предварительное типическое районирование генеральной совокупности, т.е. разбивает на группы (типы) по признакам, от которых зависят изучаемые показатели, а потом производим механический отбор. Такой способ отбора называется типическим отбором с механической выборкой.
Типический отбор часто сочетают с несколькими стадиями (ступенями) отбора. При этом каждая стадия имеет свою единицу отбора. Такая выборка называется многоступенчатой.
Многофазная выборка – отличается от многоступенчатой тем, что на всех стадиях выборки сохраняется одна и та же единица отбора.
Серийная выборка – при ее проведении производится отбор не отдельных единиц, а целых серий. Внутри отобранных серий производится сплошное обследование всех единиц.
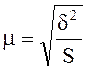 ,
,
где d2 – межсерийная дисперсия,
S – число отобранных серий.
Моментное наблюдение. На определенные моменты времени фиксируется наличие отдельных элементов изучаемого процесса. Применяется для изучения рабочего времени и времени работы оборудования. В этих случаях в момент наблюдения фиксируется, находится ли рабочий или станок в процессе работы или простое (с указанием причин).
31. Ряды динамики, Виды рядов динамики:
Ряды динамики – это статистические данные, отображающие развитие изучаемого явления во времени. Ряд динамики состоит из двух элементов:
- показателя времени (t);
- уровня ряда (y).
Виды рядов динамики:
· в зависимости от приводимых в них обобщающих показателей различают ряды динамики абсолютных, относительных и средних величин;
· в зависимости от временного параметра различают моментные ряды динамики, характеризующие уровень развития явления на определенный момент времени, и интервальные – за определенные периоды времени.
Для анализа ряда динамики необходимо приведение всех составляющих его элементов к сопоставимому виду. Несопоставимость статистических данных может быть обусловлена следующими причинами:
· территориальные изменения (увеличение границ города);
· изменение единиц измерения;
· изменение методики первичного учета.
Для приведения информации к сопоставимому виду производится смыкание рядов динамики. Для этого определяют коэффициент перерасчета, используя данные за год, в котором произошли изменения. Например:
![]() УБ 1996
УБ 1996
K = УА 1996 ,
где УА и УБ - соответственно данные до и после изменения.
Затем все данные до (1996) года изменения пересчитываются с учетом коэффициента. Получаем сомкнутый ряд.
·
32.
Средний уровень ряда для интервального ряда динамики определяется:
![]() y = ∑ уi
y = ∑ уi
где- это сумма уровней ряда;
N– число уровней.
Средний уровень моментного ряда динамики с равными интервалами:
![]() ½ y1 + y2 + …+ yn –1 + ½ yn
½ y1 + y2 + …+ yn –1 + ½ yn
y = n-1 ,
где n – число уровней ряда динамики.
Средний уровень моментного ряда с неравными интервалами (с неравно стоящими датамиA): ∑yiti
y = ∑ti ,
где ti – промежутки времени.
33
Абсолютный прирост – разность уровней ряда.
Базисный абсолютный прирост: ∆уб = уi – у0 ,
где уi– сравниваемый уровень ряда;
уо – уровень, принятый за постоянную базу.
Цепной абсолютный прирост: ∆уц = уi – уi-1 ,
где уi –1 – уровень, предшествующий сравниваемому.
Темпы роста – отношение уровней ряда одного периода к другому, выражаются в процентах и коэффициентах.
Базисные темпы роста: Тр б = (уi / у0) ·100%
Цепные темпы роста: Тр ц = (уi / уi-1) · 100% .
Темпы прироста характеризуют абсолютный прирост в относительных величинах, выражаются в процентах и коэффициентах.
Базисный темп прироста: ∆Тпр б = (∆у бi / у0) · 100% = ((уi – у0) / у0) · 100%.
Цепной темп прироста: ∆Тпр ц = (Dуцi / уi-1) · 100% = ((уi – уi-1) /уi-1) · 100%
Темп прироста можно получить из темпа роста: ∆Тпр б = Тр б – 100% ;
∆Тпр ц = Тр -100% .
Средний абсолютный прирост – обобщенная характеристика индивидуальных приростов ряда динамики.
_ _
∆уб = ∑(∆уб) / n ; ∆уц=∑(∆уц) / n .
Средний темп роста:
_ __________________ _ ______
Тр =ⁿ√ Тр 1 · Тр 2 · … · Тр n ; Тр =yn/у0 ,
где Тр 1, Тр 2, …, Тр n – индивидуальные темпы роста;
n – число индивидуальных темпов роста;
m – число уровней ряда минус 1.
Средний темп прироста:
_ _ _ _∆Тп (%) = Тр (%) – 100% , ∆Тпр = Тр – 1
34.
Для анализа ряда динамики необходимо приведение всех составляющих его элементов к сопоставимому виду. Несопоставимость статистических данных может быть обусловлена следующими причинами:
· территориальные изменения (увеличение границ города);
· изменение единиц измерения;
· изменение методики первичного учета.
Для приведения информации к сопоставимому виду производится смыкание рядов динамики. Для этого определяют коэффициент перерасчета, используя данные за год, в котором произошли изменения. Например:
![]() УБ 1996
УБ 1996
K = УА 1996 ,
где УА и УБ - соответственно данные до и после изменения.
Затем все данные до (1996) года изменения пересчитываются с учетом коэффициента. Получаем сомкнутый
35.
При анализе рядов динамики возникает необходимость выявления общей тенденции развития (тренда), исключая разного рода отклонения, вызванные
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.