Методические указания к выполнению практических занятий по дисциплине «Промышленное рыболовство», страница 11

А = 1 – 1,9563*w/(l_T – l)                                                (52)

где w - максимальная дистанция реагирования раб на трал, м.

В = 0.2079V_T/V_P                                                             (53)

                0, если В > 1, A > 0, AB > 1,

                1-0.5B, если A<0, B<1,

                0.5B, если A<0, B>1,

 P₁₂=             , если A>0, B>1, AB<1,     (54)

            1-B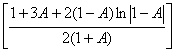 , если A>0, B<1, AB<1

4.1.5. Вероятность Р₅                   Р₅ = p/4                (55)

4.1.6. Вероятность Р₆.

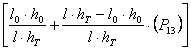Р₆ =                           (56)

где l₀h₀ = 0.159                                            (57)

где l₀ и h₀ – горизонтальное и вертикальное раскрытие мелкоячейной части трала,

      a и n – шаг и количество ячей в мелкоячейной части трала.

Р₁₃ = 0,5(Р_13В + Р_13Г)                                                (58)

Р_13В = 1 - *sin a_В                                                 (59)

Р_13Г = 1 - *sin a_Г                                                 (60)

sin a_В = (h_T – h₀) / 2L_TB                                             (61)

sin a_Г = (l – l₀) / 2L_TГ                                                 (62)

где L_TB – расстояние от гужа верхней подборы до мелкоячейной части, м.,

       L_TГ – расстояние от конца крыльев до мелкоячейной части, м..

4.1.7. Вероятность Р₇.

Р₇ = [L_T + t_T(V_T – V_P)] / V_P*t_T                                   (63)

Примечание: если расчетное значение какой-либо вероятности получится больше 1, то это означает, что данное событие достоверно и вероятность его равна 1.

4.1.8. Вероятность Р₈

Р₈ = 1 – Ф(-)                                                         (64)

m_Z = m_X – m_y                                                               (65)

s_Z =                                                            (66)

где m_X и s_X – МО и СКО максимального охвата тела рыб, мм,

       m_y и s_y – МО и СКО внутреннего размера ячеи, мм.

m_y = 3,92 а_К                                                                (67)

s_y = 0,078 а_К                                                              (68)

m_X и s_X – для некоторых рыб даны в приложении.

Необходимо отметить, что все рыбы промыслового размера должны удерживаться мешком трала, т.е. Р₈ должна равняться 1. Судя по (64), это возможно при условии, если член Ф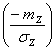 равен нулю. Это, в свою очередь, возможно, если отношение m_Z к s_Z больше или равно 4. Тогда шаг ячеи в мешке можно определить из уравнения

m_Z – 3,92а_К = 4                                     (69)