Задание 1
1. Зафиксировать расстояние h, на котором будет изменяться время t движения маятника вниз. На расстоянии h время падения t измерить 5 раз. Полученные данные занести в таблицу 1. Рассчитать среднее значение времени падения tср..
2. По формуле (3) рассчитать экспериментально полученное значение момента инерции Маятника Максвелла.
3. С помощью линейки измерить длину стержня и радиус диска. Полученные значения занести в таблицу 2.
4. По формулам (5), (6), (7) рассчитать моменты инерции оси, диска и кольца. Полученные значения занести в таблицу 2.
5. По формуле (4) рассчитать теоретическое значение момента инерции Jтеор. маятника Максвелла.
6. Сравнить теоретически вычисленное значение момента инерции Jтеор. с измеренным в пункте 2 значением Jэксп.. Для этого оценить относительную погрешность измерения момента инерции по формуле:
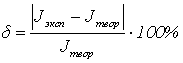 .
.
Таблица 1
Расчет экспериментального значения момента инерции Jэксп.
маятника Максвелла
|
|
|
|
|
|
|||
|
|
|||||||
|
m = … (кг) |
h = … (м) |
r = … (м) |
Jэксп. = … (кг·м2) |
||||
Таблица 2
Расчет теоретического значения момента инерции Jтеор.
маятника Максвелла
|
Наименование величины |
Масса, (кг) |
Линейные размеры |
Моменты инерции |
|
Момент инерции стержня (оси) |
l = … (м) |
JО = … (кг·м2) |
|
|
Момент инерцити диска |
R = … (м) |
JД = … (кг·м2) |
|
|
Момент инерции кольца |
R = … (м) |
JК = … (кг·м2) |
|
|
Момент инерции маятника |
Jтеор = … (кг·м2) |
||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.