


















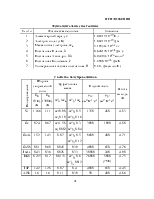


Методические указания к лабораторным работам предназначены для студентов ФРТ и ОФ по специальностям 200800 и соответствуют Рабочим программам по курсу "Физические основы микроэлектроники".
Утверждено
Редакционно-издательским советом университета
В качестве методических указаний
к лабораторным работам
© СПбГЭТУ "ЛЭТИ", 20007
Цель работы: исследование статистических свойств собственных нормальных колебаний решетки (фононных состояний); изучение функции плотности фононных состояний (мод нормальных колебаний решетки); исследование температурной зависимости теплоемкости решетки.
В работе исследуется температурная зависимость теплоемкости решетки по приближенной теории Дебая.
Теплоемкость при постоянном объеме представляет собой термодинамическую величину, определяемую выражением
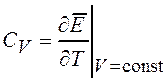 ,
,
где
![]() – средняя энергия системы.
– средняя энергия системы.
Нормальные колебания решетки являются независимыми, если для данного твердого тела справедливо гармоническое приближение и можно считать применимым закон Гука. Энергия колебаний решетки является квантованной величиной. Квант энергии упругой волны называется фононом.
Средняя энергия системы фононов при заданной температуре может быть определена исходя из общих соотношений для квантовых статистических систем:
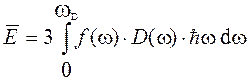 ,
,
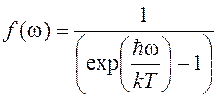 ,
,
где f(ω) – функция распределения Планка; D(ω) – плотность мод нормальных колебаний (число мод на единичный интервал частот); ħω – энергия фонона; ħ – постоянная Планка; k – постоянная Больцмана. Множитель 3 связан с учетом трех возможных типов поляризации фононов.
В континуальном (дебаевском) приближении скорость звука считается постоянной. Плотность мод D(ω) каждого типа поляризации для кубического кристалла на единицу объема в рассматриваемом приближении определяется выражением
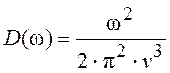 ,
,
где v – скорость звука.
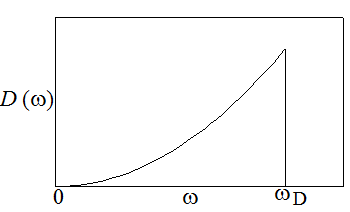
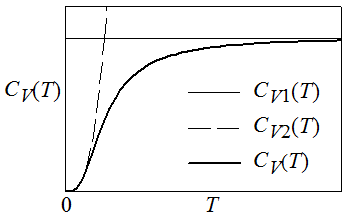
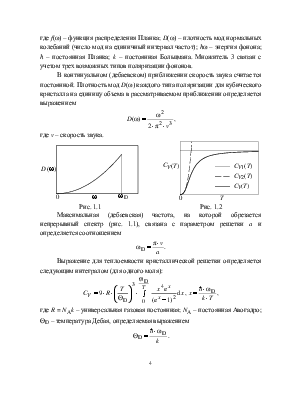
Рис. 1.1 Рис. 1.2
Максимальная (дебаевская) частота, на которой обрезается непрерывный спектр (рис. 1.1), связана с параметром решетки a и определяется соотношением
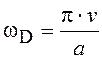 .
.
Выражение для теплоемкости кристаллической решетки определяется следующим интегралом (для одного моля):
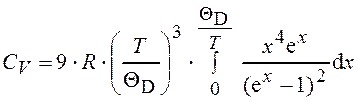 ,
, 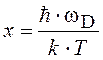 ,
,
где R = NAk – универсальная газовая постоянная; NA – постоянная Авогадро; ΘD – температура Дебая, определяемая выражением
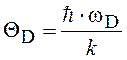 .
.
Приведенные далее соотношения позволяют определить теплоемкость кристаллической решетки в двух предельных случаях: T >> ΘD и T << ΘD соответственно (рис. 1.2):
![]() ;
(1.1)
;
(1.1)
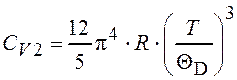 .
(1.2)
.
(1.2)
1. Оцените влияние скорости звука на плотность мод нормальных колебаний.
2. Проанализируйте изменение дебаевской частоты в зависимости от изменения скорости звука и параметра a кристаллической решетки.
3. Изучите вид температурной зависимости теплоемкости решетки. Исследуйте на нескольких примерах влияние температуры Дебая на данную зависимость.
4. Рассчитайте величины скорости звука и частоты Дебая для заданных материалов в направлениях [001], [011], [111].
1. Основываясь на материалах лекционного курса и результатах проделанной работы, объясните наблюдаемый вид зависимости D(w) в дебаевском приближении.
2. Ответьте, как и почему влияет изменение скорости звука и параметра кристаллической решетки a на величины wD и ΘD?
3. Объясните, как изменятся скорость звука и wD в анизотропном
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.