Устройство и принцип действия доплеровских измерителей скорости и углов сноса. Состав и назначение основных систем навигационных комплексов летательных аппаратов, страница 6

Если в радиотехническом Измерителе 2 применена следящая система (как это обычно и делается), то при комплексировании используют фильтрующие элементы, входящие в следящий измеритель (рис. 2.4).

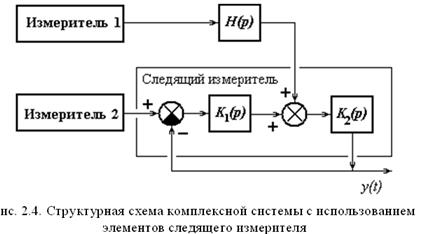
Полученная схема не вносит динамической погрешности. Рассмотренные схемы компенсации относятся к классу разомкнутых, в которых уменьшаются возникшие в измерителях погрешности. Если погрешности одного из измерителей, например Изм. 1 на рис. 2.5, возрастают с течением времени (как при измерении скорости методом интегрирования ускорения), а погрешности Измерителя 2 стационарны, применяют замкнутую схему компенсации. В такой схеме Фильтр оценивает погрешность Измерителя 1, а Корректирующее устройство устраняет причины, приводящие к накоплению погрешности этого измерителя. Для оценки применяют многомерные линейные фильтры (фильтры Калмана), реализующие на базе ЭВМ оптимальные алгоритмы обработки подаваемых на них сигналов.

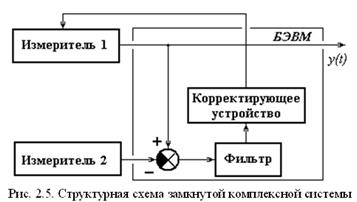
Обобщенная структурная схема комплексной навигационной системы. Рассматриваемая система (КНС) состоит из нескольких (не менее двух) разнородных измерителей одного и того же элемента W, объединенных бортовой ЭВМ (БЭВМ). Эта БЭВМ оценивает составляющие погрешности одного из измерителей, принятого в данной системе за основной, и корректирует эти погрешности или устраняет вызывающие их причины. В качестве основного измерителя обычно используется инерциальная навигационная система (ИНС), в которой отсутствуют фильтры, ограничивающие ее быстродействие. Это обстоятельство, а также то, что инерциальный измеритель разомкнут по отношению к измеряемому элементу W, обусловливает практическое отсутствие динамических погрешностей ИНС. Так как схема комплексирования не вносит дополнительных динамических погрешностей, то и КНС будет обладать хорошими динамическими свойствами.

Основным элементом КНС является многомерный дискретный линейный фильтр Калмана. На фильтр подается процесс z = x₁ – х₂, где х₁ и х₂ – погрешности комплексируемых измерителей. При формировании алгоритма оптимальной обработки х₁ и х₂ представляются линейными стохастическими дифференциальными уравнениями n-го порядка, описывающими поведение составляющих погрешностей во времени. Такое представление эквивалентно записи погрешностей в виде вектора состояния  размером (n´1). При этом процесс z также записывается в виде вектора  размером (m´1), где m — число скалярных измерений на входах фильтра.

Рассмотрим в качестве примера КНС определения скорости летательного аппарата по данным ИНС и доплеровского измерителя скорости (ДИС) (рис. 2.6).

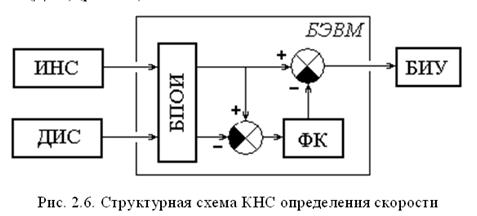
Основным измерителем здесь является ИНС. Информация о трех составляющих вектора скорости в цифровой форме подается на блок предварительной обработки БПОИ, в котором синхронизируется частота поступления информации в фильтр Калмана ФК. Очевидно, что информация на ФК должна подаваться дискретно с интервалами, достаточными для выполнения цикла вычислений в фильтре. Сигнал измерений фильтра формируется путем образования разностей соответствующих составляющих вектора скорости, измеренных ИНС и ДИС. Поэтому в рассматриваемом случае вектор  имеет размер (2´1). Вектор  включает основные составляющие погрешности ИНС и ДИС. Порядок системы дифференциальных уравнений, описывающих погрешности ИНС, а следовательно, и число учитываемых при построении КНС составляющих, входящих в вектор , определяется требуемой точностью компенсации. С учетом двух составляющих погрешности ДИС (по двум компонентам скорости) общее число составляющих вектора  может доходить до 10…15.

Фильтр Калмана в данной системе выдает оценки погрешностей ИНС по скорости DV_x,y на основе заложенной в фильтр априорной информации о поведении погрешностей во времени (матрица Ф) и о шумах измерения. Скорректированные значения составляющих горизонтальной скорости поступают от ИНС в блок индикации и управления БИУ. При небольшом усложнении данная КНС может быть использована и для определения местоположения ЛА.