Туннельный эффект. Энергетический спектр водородоподобного атома, страница 2

Существует несколько, различного рода приближений, которые дают возможность сложную задачу свести к простой. Главгая идея приближения заключается в использовании физического смысла волновой функции. Мы будем говорить о том что оператор Гамельтона. Напомним что:

;, волновая функция является функцией большого чисола электронов, все электроны будут различаться по их радиус векторам, массив из I электронов, и все реакции будут иметь индексы . -это решение уравнение Шредингера для I электронов и  ядер. Система очень смложная потому что:

1.  Электроны обладают множеством взаимодействий между собой

2.  Есть Кулоновское взаимодействие между ядрами

3.  Есть Кулоновское между электронами и ядрами

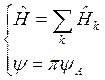Это все потенциальная энергия взаимодействия, есть кинетическая энергия движения электронов и кинетическая энергия движения ядер. То есть если это расписать то это получается очень грамоздкая сложная система уравнений. Так вот идея упрощение решения заключается в том, что мы будем говорить о следующем: что наш сложный оператор который является функцией К состояний колическтва частиц, может быть представлен как сумма по всем. Полный Гамельтониан системы будет равен сумме Гамельтонианов, если эта система состоит из К подсистем. Придумаем такое приближение которое разрешает разделить сложную систему на некоторое количество подсистем. Допустим что их будет К, и тогда можно зная как выглядит Гамельтониан для отдельных систем, сложить и найти то что нас интересует. Тогда для волновой функции мы будем иметь произведение по всем решениям соответствующих операторов. И так многочастичную задачу нужно упростить и вот это идея упрощения. И здесь существует несколько приближений. Мы рассматриваем  ядра, но все эти ядра представляют собой водородопообные атомы. Поэтому первое приближение связано с рассмотрением самого потенциального рельефа одгого атома, и это будет водородоподобный атом. Задача которую мы рассмотрели имеет следующие приближения:

1.  Адиабатическое приближение. Оно использует простой физический факт. Электроны по сравнению с ядрами являются очень подвижными, поэтому  можно рассматривать движущийся электроны в поле квази неподвижных ядер. То есть всю много частичную задачу сразу делим на две, для электронов и для ядер. И это связано с тем что масса электрона много меньше массы ядра. Теперь мы будем имень отдельно электронный Гаменьтониан волновой функции и ядерный Гаменьтониан, но есть некий потенциал взаимодействия электронов и ядер, который сшивает эти два приближения. Но так как нас интересует волновая функция и вся энергетика электоронов, дальше мы занимаемся поиском упрощения Гамельтониана для электронов. Нам нужно найти такой способ что бы его представить как сумму. То есть Гамельтониан взаимодействующих электронов равен сумме Гамельтонианов для каждого из электронов, а они взаимодействуют по Кулону. Вот здесь есть другое приближение которое так и называется – одноэлектронное приближение.

2. 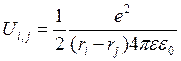 Одноэлектронное приближение. Выбираем i,j электрон и они взаимодействуют по Кулону. Запишем потенциальную энергию i,j электрона. И вместо папарного взаимодействия i,j электрона мы будем выбирать любой электрон (пусть его номер К), который двигается в поле всех оставшихся электронов. Не попарное взаимодействие всех электронов а выбираем какой то электрон К и смотрим как он взаимодействует с полем всех оставшихся электронов, но так ка эта идея должна работать для любого номера К, какой бы мы не взяли, то говориться что поле оставшееся должно быть самосогласовано с выбором. Тогда потенциал U_i,j самозаменяется на некоторый самосогласованный потенциал и будем обозначать . Самосогласованный потенциал – место потенциальной энергии взаимодействия попарного для электронов. Мы рассматриваем взаимодействие К электрона со всеми остальными, а потом суммируем по всем этим состояниям.

Адиабатическое приближение                                       Одноэлектронное приближение

Для оператора Н_i, для отдельно взятого электрона, теперь будем иметь:

 - оператор его кинетической энергии

 - оператор самосогласованного поля

 - оператор, который учитывает взаимодействие электронов с ядрами

Просуммируем все по I электронам. Оказывается что потенциальный рельеф взаимодействия электронов, заданной в самосогласованном поле и оставшейся потенциальный рельеф взаимодействия I электрона с ядром, можно качественно, очень легко описать. И это будет потенциальная энергия I электрона. Все атомы у нас одинаковы, водородоподобные. Все находятся на одной оси r. Рассматриваем одномерный кристалл, период трансляции а, и нарисуем потенциальный рельеф. Нарисуем потенциальный рельеф для 2 атома считая, что 1 и 3 отсутствуют. Введенный метод суперпозиций применим для атома 1 и 3. Задача у нас уходит на плюс, минус бесконечность. А теперь рассматривая вес пространство потенциального рельефа, мы видим места где остается потенциальный рельеф заданного атома, а есть места где происходит взаимодействие потенциального рельефа. Атомы электрона 2 начинают взаимодействовать с ядром атома 3 и наоборот. Вот это приводит к так называемому обменному взаимодействию, то есть мы находим результирующую потенциального рельефа. Мы будем иметь картину из периодически повторяющихся потенциальных полей.