Туннельный эффект. Энергетический спектр водородоподобного атома

Лекция 6.

Решение уравнения Шредингера является волновая функция, которая есть не что иное как Де Бройля. Волна Де Бройля это волна которая описывает свободу частиц, а не воздействие на них.

Мы будем говорить о квазисе свободной частицы. Она находится в таком потенциальном ящике, но самый главный вывод для решения этой потенциального ящика или ямы, это то что поверхность частицы квантуется, то есть значение волнового эффекта K, и имеет размерность  где n=1,2,3,…Частица может находиться в одном из своих квантовых состояний. Все квантовые состояния отличаются значением модуля волнового вектора, то есть значением К_н. Само выражение 7  которое описывает волновую функцию, и квадрат модуля говорит о вероятности найти частицу в том или ином состоянии. И когда мы просуммируем вероятность по всем состояниям, нужно понимать что частица находится в одном из своих состояний.

Туннельный эффект

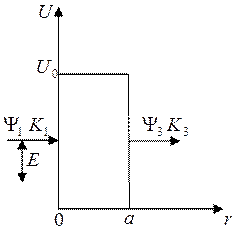Представим, что у нас потенциальный барьер задан, как показан на рисунке. У нас есть некий потенциальный барьер, для простоты возьмем прямоугольной формы. Высота U₀, параметры барьера (0,а), и пускай частица падает слева, и она обладает некоторой кинетической энергией.

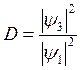Туннельным эффектом называется явление прохождения квантовой частицей потенциального барьера без изменения потенциальной энергии. То есть, если у нас есть волновая частица вероятность, которой , которая имеет волновой вектор К₁, она двигается в направлении r, на пути этой частицы потенциальный барьер. Можно утверждать о том, что есть некоторая вероятность того, что эту частицу мы увидим за потенциальным барьером, в состоянии  с волновым вектором К₃. Для того, что бы найти: а на сколько вероятно найти частицу за барьером? Мы находим такой параметр, который называется прозрачностью потенциального барьера D. Прозрачность потенциального барьера найти очень просто: вероятность найти частицу за барьером, с волновой функцией , к вероятности найти частицу до барьера . Так вот если мы найдем это отношение, то мы определяем коэффициент прозрачности этого потенциального барьера, обладающим туннельным эффектом. Если ввести область с  некой вероятностью , и происходит сшивание на границе разделов. И в результате получается во такое выражение для прозрачности потенциального барьера:

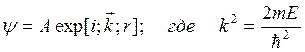
k – волновой вектор

Мы говорим о туннельном эффекте, когда кинетическая энергия частицы меньше чем высота потенциально барьера. Если энергия будет выше, то проблем для прохождения потенциального барьера частице, но она, конечно, будет чувствовать присутствие этого барьера. Мы будем рассматривать тот случай, когда кинетическая энергия меньше чем высота потенциального барьера. Рассмотрим явление наведенной поляризации. Допустим, что у нас есть диэлектрическая среда, диэлектрик. Но если у нас есть движение свободного электрического заряда слева и справа, то движение левого электрического заряда приведет к движению электрического заряда справа. Все квантовые частицы тождественны. Этот электрон как бы проходит насквозь, но все это будет связано с толщиной диэлектрической стенки, то есть можно говорить о явлении наведенной поляризации, только тогда, когда есть конечная толщина стенки. Мощность потенциального барьера это произведение ширины барьера на величину потенциальной энергии, то есть на высоту.

Мощность потенциального барьера может быть постоянной, у нас может расти высота, а уменьшаться ширина, или наоборот.

Энергетический спектр водородоподобного атома

Водородоподобным атомом называется атом, который обладает сферической симметрией. Это  хорошо выполняется для проводящих металлов и щелочных металлов. У атома водорода всего одна электронная орбита, а у водородоподобного может иметь сколько угодно, для того, что бы скомпенсировать заряд ядра.

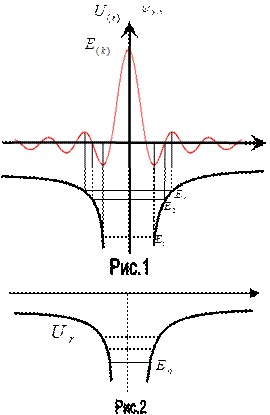
Энергетический спектр водородоподобного атома, рассмотрим рис. 1. Это есть результат решение уравнения Шредингера для такого атома. На рисунке мы видим зависимость U(r), это потенциальная энергия электрона находящаяся на некотором расстоянии от ядра. И эта потенциальная энергия имеет воронко образный рельеф. Потенциальная яма не такая прямоугольная, которая была у нас, а имеет такие скосы как показаны на рис. 2

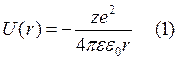
Мы имеем вот такой вид потенциального рельефа, и так же как для бесконечно потенциальной ямы с квантовыми состояниями.

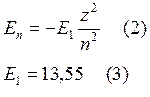
В зависимости от номера оболочки и квантовых чисел (n,l,m,s). n – главное квантовое число которое определяет контование, физический смысл его тот же самый что и бесконечно глубокой потенциальной яме с плоским дном. То етсь у нас есть различные уровни Е_n, где n – номер квантового состояния. По Бору n – это орбита, номер орбиты такой что у вас на длинне окружности , укладывалось бы целое число пол Де Брой. См рис.3. И именно этим определяется радиус квантования. l – орбитальное. m – магнитное квантовое число и  s – спиновое число.

Уравнение Шредингера для кристалла

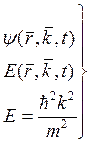Искомой функцией является нахождение собственных значений оператора Габельтона, и соответственно собственных функций. Нам надо знать вероятность нахождения в данной точке пространства в данный момент времени, ну и какой волновой функцией описывается и какой вектор, а так же знать соответствующее значение энергии Е.

Итак, наша задача раасмотреть крислалл, решить уравнение Шредингера для кристалла, для того что бы, для свободных электронов в кристалле найти все вот эти функции. Уравнение Шредингера для кристалла задается для большого колическва частиц.