Теплоёмкость. Сфера Дебая. Фонон и фононное рассеяние

Лекция 14

Теплоёмкость

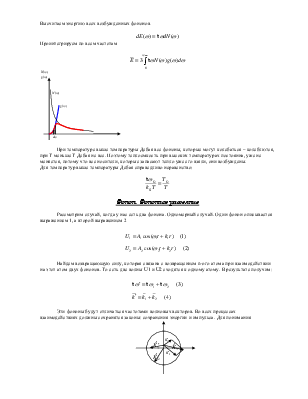
Впервые эту задачу рассмотрел Дебай. Теплоёмкость это параметр, который определяет скорость изменения внутренней энергии системы при изменении температуры. У нас есть фононный газ. Фонон обладает энергией и импульсом.

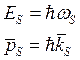
Фонон представляет собой квази частицу, то есть частицу, которой нет, она придумана. Максимальное число S это количество атомов нашей цепочки. Просуммируем энергию всех возбужденных фононов.

Принято фонон, квази частицу, считать имеющую спин 0, и химический потенциал должен быть равен нулю, который является внутренним состоянием частиц.

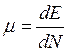
Система фононов всегда находится в тетрадинамическом равновесии. Поэтому производная равна нулю.

Распределение Планка

Оно говорит о среднем числе частиц, фононов, которые являются функциями частоты от  при заданной температуре.

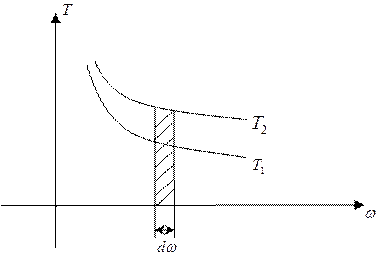
Сфера Дебая

Имеем некую область, ограниченную сферой, назовем её сферой Дебая. Физический смысл заключается в том, что внутри сферы каждый из векторов определяет какой то фонон.

Высчитаем энергию всех возбужденных фононов

Проинтегрируем по всем частотам

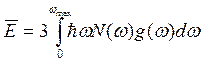
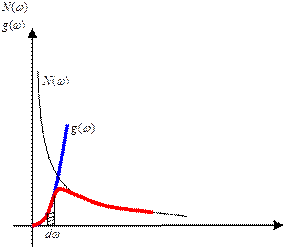
При температуре выше температуры Дебая все фононы, которые могут колебаться – колеблются, при Т меньше Т Дебая не все. Поэтому теплоемкость при высоких температурах постоянна, уже не меняется, потому что все носители, которые запасают тепло уже его взяли, они возбуждены.

Для температур выше температуры Дебая справедливо неравенство:

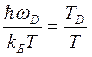
Фонон. Фононное рассеяние

Рассмотрим случай, когда у нас есть два фонона. Одномерный случай. Один фонон описывается выражением 1, а второй выражением 2

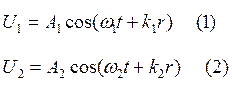
Найдем возвращающую силу, которая связана с возвращением n-ого атома при взаимодействии на этот атом двух фононов. То есть две волны U1 и U2 сходятся к одному атому. В результате получим:

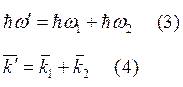
Эти фононы будут отличаться частотами волновых векторов. Во всех процессах взаимодействиях должны сохранятся законы: сохранения энергии и импульса. Для понимания

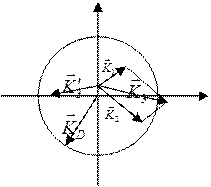
взаимодействия двух фононов, достаточно рассмотреть сферу Дебая.

У нас есть 2 фонона, каждый из которых характеризуется некой точкой. Дальше они начинают взаимодействовать. Мы должны найти К3 которое равно векторной сумме К1 и К2. В зависимости от того чему равна величина волнового вектора , после взаимодействия, мы и различаем два случая:

1. К₃<К_д – нормальный процесс

2. К₃>К_д – процесс  переброса

При процессах взаимодействия, в процессах рассеивания , при направленном движении носителей, должны выполняться законы для фонона. 

Время релаксации

- вероятностная величина, а величина обратная  есть ни что иное, как частота столкновений. Число столкновений зависит от числа рассеивающих центров. Сделаем вывод того что: время свободного пробега обратно пропорционально числу рассеивающих центров.

При низких температурах, фононы обладают малой частотой и малым волновым вектором. Если волновой вектор мал, то длина волны большая. Поэтому при низких температурах, рассматривают взаимодействие фононов с препятствиями.