Тензор. Симметрия кристаллической структуры. Дислокация

Лекция 4

Тензор

Анизотропия свойств описывается с помощью тензоров.

Тензор - это некая математическая величина, которая связывает …. и воздействие на кристалл, если этот кристалл анизотропен. На примере диэлектрической проницаемости атома возникает поляризация связанная с распространением кристалла. К вектору поляризации добавляется вектор, напряженности электрического поля, дает нам отклик в виде вектора D не совпадающим с E.Каждая компонента этого тензора имеет ту же самую размерность и физический смысл, что и диэлектрическая проницаемость (Ф/м).

Тот факт, что симметрия структура кристалла отражает симметрию анизотропных свойств связанное с симметрией самого тензора. Напомним, что тензор имеет определенное число компонентов. Число компонент тензора определяется тройкой в степени n (что называется рангом тензора).n может принимать любые значения, например, если n=0, то N=1 (ск); если n=1, то N=3 (вектор); если n=2, то N=9 и это тензор второго порядка, и в зависимости от структуры кристалла у нас получается разная симметрия тензора.

Важным параметром симметрии кристалла является так называемая указательная поверхность. Указательная поверхность она показывает чему равно свойство кристалла в заданном направлении. Для этого нужно измерить искомое свойство, в частности диэлектрическая проницаемость, подавая этот вектор в разные направления кристалла. Для тензора второго порядка указательная поверхность представляет собой уравнение второго порядка, в частности эллипсоид. По осям координат обычно откладываются значения равные единица делить на корень а_ij.

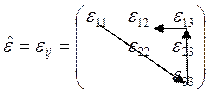Если у нас воздействие, в данном случае напряженность электрического поля, направлены по главным осям то они так и обозначаются.

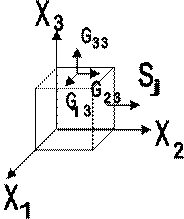Что такое напряжение, это практически отношение силы к площади поперечного сеченияесли этоскалярная величина. Рассмотрим это все на примере кубика нарисованного в координатных осях. Это т вектор у нас может быть приложен по осям Х1, Х2, Х3. Значит значени i, j= 1,2,3, а S обычно характерезуется площадью. Задается вектор перпендикулярной заданной площади. Поэтому если кристалл анизотропен, то деформация может быть F_i=G_ij*S_j , то есть  мы на каждой площадочке будем иметь три разных направления, и это есть полевой тензор.    

Дефекты структуры

На самом деле мы нигде не сталкиваемся с идеальными кристаллами, мы имеем дело с ними только на бумаге. А в реальности у нас всегда есть дефекты структуры, либо которые появились в результате кристаллизации, либо дефекты которые сами создали себя.

Симметрия кристаллической структуры

Все дефекты структуры классифицируются по размерности: точечные, протяженные и линейные. Размеры точечного дефекта соизмеримы с размерами элементарной ячейки. Линейные дефекты, как правило, возникают за счет некоторого сбора точечных дефектов. Но вот если эти точечные дефекты выстраиваются в линию, то они образуют линейный дефект и про них говорят, что дислокация точечных дефектов. И так третий вид дефектов это поверхностные дефекты, как правило, это поверхность зерна кристалла. А зерно с ярко выраженной ориентацией называют кристаллитом.

Точечные дефекты бывают двух типов, но эти два типа потом будут сильно различаться.

Первый тип, это когда есть лишний атом в решетке. Это атом может быть по-разному встроен в решетку. Если этот атом введен специально, то он будет нести лидирующую функцию, и создает интересные, нужные свойства для нас. Так вот этот примесный атом может быть встроен в решетку, так что замещает основной атом. И он будет существенно искажать нашу решетку, если его размеры отличаются от основных, либо много меньше, либо много больше.

Второй случай, когда атом внедряется в решетку, такой атом называется примесным.

Третий случай называется вакансией. Это тот момент, когда в кристаллической решетке отсутствует атом – дырка (пустота). И соответственно нарушается связь между соседними атомами, и образуются вакансии.

Если в кристалле есть области с любой из деформаций то, как правило, все эти деформированные области будут стремиться в одно место. Следовательно, будут возникать механические напряжения,  а система должна находиться в таком состоянии, что бы собственная потенциальная энергия была минимальная. То есть система постоянно стремиться к минимизации и создает такие условия, что структура начинает двигаться.

Кристалл, как правило, растет от внешних воздействий, и всегда возникают какие либо дефекты в структуре. Симметрия кристалла является симметрией его самого, и симметрии воздействия. Так вот это внешнее воздействие оно всегда есть.  

Дислокация

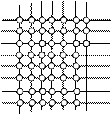
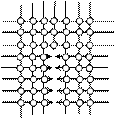Дислокация бывает двух типов: одна краевая, а вторая винтовая.

Как образуется краевая дислокация. Представим, что у нас есть идеальный кристалл, в нем есть 3 вакансии, то есть в кристалле образовалась пустота, но как мы знаем в кристалле пустоты не бывает и соседние атомы начинаю взаимодействовать и в результате происходит перестройка в нашей структуре. Соседние атомы занимают место вакансий, и происходи поэтапный сдвиг атомов. Например, если мы имеем царапину на поверхности, то со временем она уйдет во внутрь. Такая дислокация называется краевой.

Винтовая дислокация. Рассмотрим на примере плоскости, значит “надрываем” эту плоскость и один край поднимаем вверх, а другой опускаем вниз. И если на это посмотреть сверху то получается винт. Значит, взяли структуру и нарезали и сместили на величину равную параметру трансляции.

Количественный параметр, характеризующий вектор дислокации Бюргерса. У нас есть область деформации, на некотором расстоянии от нее мы начинаем обход, по часовой стрелке. При этом мы должны точно выдержать число шагов вниз, влево, вправо, вверх. Значит, идем вниз на 3, влево на 3, вверх на 3 и вправо на 3 и не возвращаемся в исходную точку. Вот этот вектор, который замыкает наш путь, называется вектором Бюргерса, а путь петля Бюргерса. Для линейных и линейных дислокаций характерно разное расположение вектора Бюргерса, то есть для краевой дислокации вектор перпендикулярен оси дислокации, а для винтовой, мы смещаемся вверх, он параллелен.

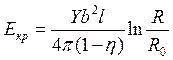
Y – Модуль Юнга

b² – Квадрат модуля Бюргерса

l – Длинна дислокации

 - Модуль всестороннего сжатия, или модуль Пуассона, то есть когда растягивают кристалл он еще одновременно сжимается, и если это сжатие значимое, то учитывается этот коэффициент.

R – Радиус вектор выбранной нами точки

R₀ – радиус ригранности, он говорит о том сколько элементарных ячеек деформируемо.

Мы всегда имеем дело с наличием дефектов в кристалле, иногда это надо, а иногда нет. Создание нужных дефектов кристалла используется для обеспечения механической прочности.