Список экзаменационных вопросов и ответы на № 1-66 по дисциплине "Математический анализ" (Введение в математический анализ. Интегрирование рациональных функций)

Последовательность {x_n} называется возрастающей, если для любого  выполняется неравенство . (если , то последовательность - убывающая). Если все элементы последовательности {x_n} равны одному и тому же числу с, то ее называют постоянной.

Возрастающие, убывающие и постоянные последовательности – монотонные.

4. Число е.

Теорема Вейерштрасса. Всякая монотонная ограниченная последовательность имеет предел.

Рассмотрим последовательность .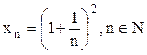

По формуле бинома Ньютона:

Пусть , тогда:

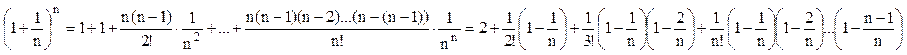
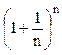 - возрастающая последовательность, причём 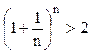. Заменим в правой части скобки на 1, а факториалы на степени двойки. По формуле суммы членов прогрессии найдём, что:

Последовательность ограничена, при этом для выполняется неравенство: 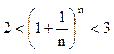, следовательно на основании теоремы Вейерштрасса последовательность имеет предел, обозначаемей буквой е.

.

Число е называется неперовым числом. Число е иррациональное, его приближенное значение равно 2,72 (е = 2,718281828459045…). Число е принято за основание натуральных логарифмов ()

5. Связь натурального и десятичного логарифмов.

За основание натуральных логарифмов принято число е, десятичных – 10. (,)

По определению логарифма имеем . Прологарифмируем по основанию 10.

Пользуясь десятичными логарифмами, находим , значит , либо

6. Предел функции в точке.

Определение 1 (на “языке последовательностей”, или по Гейне). Пусть функция  определена в некоторой окрестности точки , кроме, быть может, самой точки . Число А называется пределом функции  в точке  (или при ), если для любой последовательности допустимых значений аргумента , сходящихся к числу  (т.е. ), последовательность соответствующих значений , сходится к числу А (т.е. ).

Определение 2 (на “языке ”, или по Коши). Пусть функция  определена в некоторой окрестности точки , кроме, быть может, самой точки . Число А называется пределом функции  в точке  (или при ), если для любого положительного  найдётся такое положительное число , что при всех x, удовлетворяющих неравенству , выполнится неравенство .

7. Предел функции при стремлении аргумента к бесконечности.

Пусть функция  определена на промежутке . Число А называется пределом функции  при , если для любого положительного  существует такое число , что для всех , удовлетворяющих неравенству , выполнится неравенство .

8. Основные теоремы о пределах.

1) Предел суммы (разности) двух функций равен сумме (разности) их пределов.

Пусть ,Тогда по теореме о связи функции, ее предела и б.м.ф. можно записать  и . Следовательно, . Здесь  - б.м.ф., как сума б.м.ф. По теореме о связи функции, ее предела и б.м.ф. можно записать , т.е.

2) Функция имеет только один предел при

Пусть ,Тогда по предыдущей теореме , отсюда А = В.

3) Предел произведения (частного) функций равен произведению (частному) их пределов.

Доказательство аналогичного 1.

4) Постоянный множитель можно выносить из под знака предела.

5) Предел степени с натуральным показателем равен той же степени предела.

9. Бесконечно малые функции.

Функция  называется бесконечно малой при , если .

Б.м.ф. часто называют бесконечно малыми величинами или бесконечно малыми; обозначают обычно греческими буквами  и т.п.

Алгебраическая сумма б.м.ф. есть б.м.ф.

Произведение ограниченной функции на б.м.ф. есть б.м.ф.

10. Свойства бесконечно малых функций.

Функция  называется бесконечно малой при , если .

Алгебраическая сумма б.м.ф. есть б.м.ф.

Пусть  и  - две б.м.ф. при . Это значит, что , т.е. для любого , а значит, и  найдется число , такое, что для всех х, удовлетворяющих неравенству , выполняется неравенство . Тоже самое проделаем для  (, )

Пусть  - наименьшее из чисел  и . Тогда для всех х, удовлетворяющих неравенству , выполняются  неравенства  и , следовательно имеет место соотношение , таким образом , т.е.  - б.м.ф. при

Произведение ограниченной функции на б.м.ф. есть б.м.ф.

Пусть функция  ограничена при . Тогда существует такое число , что  для всех х -окрестности точки . И пусть  - б.м.ф. при . Тогда для любого , а значит и , найдется такое число , что при всех х, удовлетворяющих неравенству , выполняется неравенство

Пусть  - наименьшее из чисел  и . Тогда для всех х, удовлетворяющих неравенству , выполняются  неравенства  и , следовательно, . А это означает, что  - б.м.ф. при

11. Бесконечно большие функции и их связь с бесконечно малыми.

Функция  называется бесконечно большой при , если для любого числа , существует число , такое, что для всех х, удовлетворяющих неравенству , выполняется неравенство .

Если функция  - бесконечно малая (), то функция  есть бесконечно большая функция (и наоборот).

12. Сравнение бесконечно малых функций.

Две б.м.ф сравниваются между собой с помощью их отношения. Пусть  и  есть б.м.ф. при , т.е.  и .

1) Если  , то  и  называются бесконечно малыми одного порядка.

2) Если , то  называется бесконечно малой более высокого порядка, чем .

3) Если , то  называется бесконечно малой более низкого порядка, чем .

4) Если  не существует, то  и  называются несравнимыми бесконечно малыми.

Такие же сравнения и для случаев, когда ,

13. Свойства эквивалентных бесконечно малых.

1) Предел отношения двух б.м.ф. не изменится, если каждую из них заменить эквивалентной бесконечно малой.

Пусть  и  при , тогда

2) Разность б.м.ф. есть б.м.ф. более высокого порядка, чем каждая из них.

Пусть  при , тогда , аналогично

3) Сумма конечного числа б.м.ф. разных порядков эквивалентна слагаемому низшего порядка.

Пусть  и  есть б.м.ф. при , причём  - б.м.ф. высшего порядка, чем , т.е. .

Тогда , следовательно,  при .

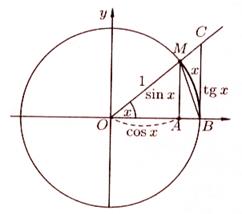
14. Первый замечательный предел.

 - первый замечательный предел

15. Второй замечательный предел.

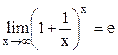 - второй замечательный предел

Мы знаем, что числовая последовательность 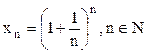 имеет предел, равный