




Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ»
кафедра РС
Дополнительное домашнее задание
«Расчет точностных характеристик системы синхронизации»
Вариант 3.
Выполнил: Терентьева А.В.
гр.8101
Проверил: Соколов А.И.
Санкт-Петербург 2011
Задана передаточная функция разомкнутой
системы 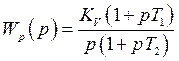 , где
, где ![]() .
.
Согласно варианту задания, N=3, тогда ![]()
![]() .
Двустороняя спектральная плотность мощности шума на входе ФФ
.
Двустороняя спектральная плотность мощности шума на входе ФФ![]() , уход фазы
синхронизирующего генератора наблюдается на фоне аддитивного белого шума
, уход фазы
синхронизирующего генератора наблюдается на фоне аддитивного белого шума![]() .
.
Т.о.
передаточная функция разомкнутой системы приобретает вид 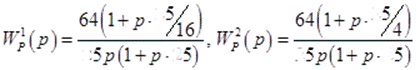
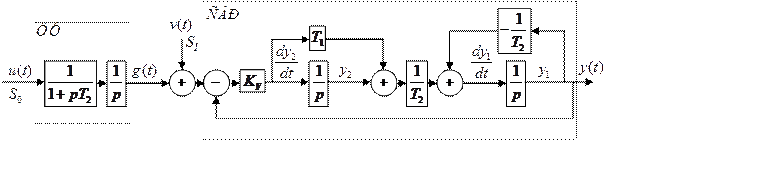
Пункт 1. Построим ЛХ и переходные процессы для исследуемых систем.

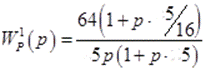

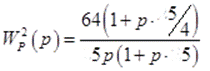
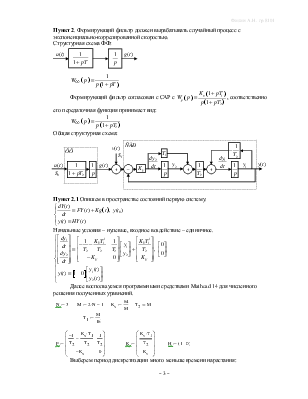
Пункт 2. Формирующий фильтр должен вырабатывать случайный процесс с экспоненциально-коррелированной скоростью.
Структурная схема ФФ:
 |
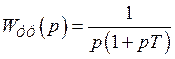
Формирующий фильтр согласован с САР с 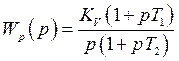 , соответственно его передаточная функция
принимает вид:
, соответственно его передаточная функция
принимает вид:
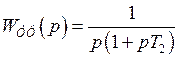
Общая структурная схема:
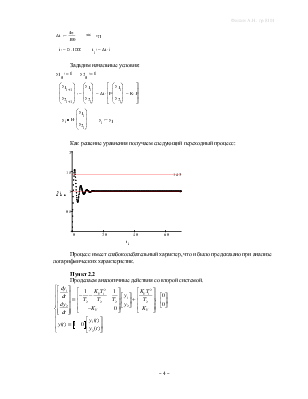
Пункт 2.1 Опишем в пространстве состояний первую систему.
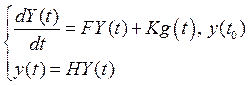
Начальные условия – нулевые, входное воздействие – единичное.
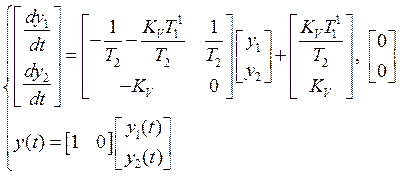
Далее воспользуемся программными средствами Mathcad 14 для численного решения полученных уравнений.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выберем период дискретизации много меньше времени нарастания:
|
|
|
<< |
|
|
|
|
|
|
Зададим начальные условия:
|
|
|
|
|
|
|
|
|
|
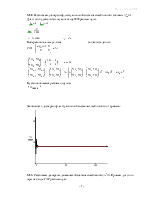
Как решение уравнения получаем следующий переходный процесс:
|
|
Процесс имеет слабоколебательный характер, что и было предсказано при анализе логарифмических характеристик.
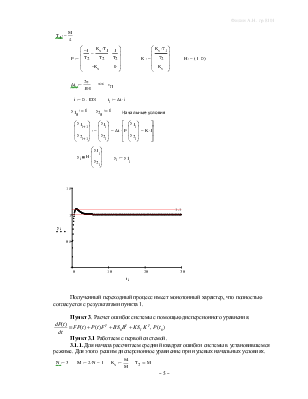
Пункт 2.2
Проделаем аналогичные действия со второй системой.
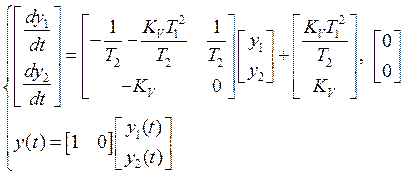
|
|
|
|
|
|
|
|
|
|
|
<< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
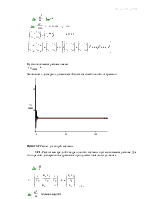
Полученный переходный процесс имеет монотонный характер, что полностью согласуется с результатами пункта 1.
Пункт 3. Расчет ошибок системы с помощью дисперсионного уравнения.
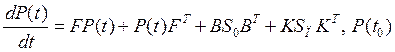
Пункт 3.1 Работаем с первой системой.
3.1.1. Для начала рассчитаем средний квадрат ошибки системы в установившемся режиме. Для этого решим дисперсионное уравнение при нулевых начальных условиях.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
<< |
|
|
|
|
|
|
|
|
|
|
|
|
При решении уравнения получаем средний квадрат установившейся ошибки системы:
|
|
|
|
3.1.2.
Рассчитаем
дисперсию флюктуационной составляющей ошибки системы ![]() .
Для этого будем считать шум на входе ФФ равным нулю.
.
Для этого будем считать шум на входе ФФ равным нулю.
|
|
|
|
|
|
|
|
|
|
Выберем начальные условия согласно заданию:
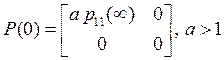
|
|
|
|
|
|
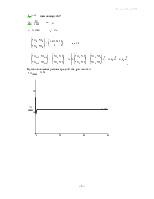
В установившемся режиме получим
|
|
Зависимость дисперсии флюктуационной составляющей ошибки от времени:
|
|
3.1.3.
Рассчитаем дисперсию
динамической составляющей ошибки ![]() . Примем
для этого шум на входе САР равным нулю.
. Примем
для этого шум на входе САР равным нулю.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
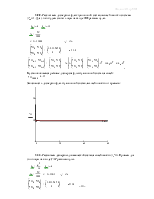
В установившемся режиме имеем:
|
|
Зависимость дисперсии динамической составляющей ошибки от времени:
|
|
Пункт 3.2 Расчет для второй системы.
3.2.1. Рассчитаем средний квадрат ошибки системы в установившемся режиме. Для этого решим дисперсионное уравнение при нулевых начальных условиях.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
<< |
|
|
|
|
|
|
|
|
|
|
|
|
В установившемся режиме средний квадрат ошибки:
|
|
|
|
3.2.2.
Рассчитаем дисперсию флюктуационной составляющей ошибки системы ![]() . Для этого будем считать шум на входе ФФ
равным нулю.
. Для этого будем считать шум на входе ФФ
равным нулю.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В установившемся режиме дисперсия флюктуационной составляющей:
|
|
Зависимость дисперсии флюктуационной составляющей ошибки от времени:
|
|
3.3.3. Рассчитаем дисперсию динамической
составляющей ошибки ![]() . Примем для этого шум на входе САР равным
нулю.
. Примем для этого шум на входе САР равным
нулю.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В установившемся режиме:
|
|
Зависимость дисперсии динамической составляющей ошибки от времени:
|
|
Пункт
4. Расчет
![]() и
и ![]() в
установившемся режиме с помощью частотных методов анализа.
в
установившемся режиме с помощью частотных методов анализа.
Пункт 4.1. Работаем с первой системой.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.о. для первой системы результаты расчетов во временной и частотной областях полностью совпали.
Пункт 4.2. Работаем со второй системой.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т.о. для второй системы результаты расчетов во временной и частотных областях также совпали.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.