Радиотехнические цепи и сигналы: Методические указания к выполнению курсовой работы

Здесь  — спектральная функция входного детерминированного сигнала,  — комплексный коэффициент передачи цепи, связанный с ее импульсной реакцией преобразованием Фурье.

При прохождении случайного сигнала через линейную цепь энергетический спектр и КФ выходного сигнала определяются следующим образом:

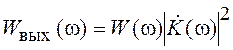,                                          (2.14)

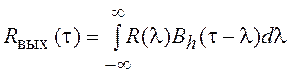,                                     (2.15)

где  и  — соответствующие характеристики входного случайного сигнала;  — корреляционная функция импульсной реакции цепи:

.

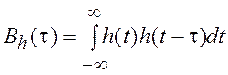Частотно-избирательную систему, выполняющую обработку аддитивной смеси (суммы) сигнала и шума наилучшим, в соответствии с тем или иным критерием, образом, называют оптимальным линейным фильтром.

В задачах обнаружения известного по форме сигнала в качестве такого критерия используют критерий максимума отношения с/ш на выходе. Если помехой является стационарный случайный сигнал в виде белого шума, то комплексный коэффициент передачи фильтра, максимизирующего отношение с/ш, определяется следующим образом:

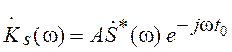,                                       (2.16)

где  — спектральная плотность входного сигнала; А — константа (коэффициент), имеющая размерность, обратную размерности спектральной плотности;  — момент времени, в который отношение с/ш на выходе фильтра достигает максимума.

Фильтр, обладающий частотной характеристикой вида (2.16), называют согласованным. Необходимым (но недостаточным) условием физической реализуемости согласованного фильтра является неравенство , где Т — длительность входного детерминированного (полезного) сигнала. Используя (2.16), можно показать, что импульсная реакция согласованного фильтра  имеет следующий вид:

,                                        (2.17)

где  есть зеркально отображенная относительно оси ординат и сдвинутая по оси времени на интервал   копия входного сигнала .

При подаче сигнала  на вход согласованного с ним фильтра на выходе фильтра появится определяемый из (2.5), (2.13) и (2.16) или из (2.12) и (2.17) сигнал

,                                     (2.18)

где  — корреляционная функция входного сигнала. Таким образом, отклик фильтра на согласованный с ним сигнал совпадает по форме с КФ последнего. Как следует из (2.18), вне зависимости от формы входного сигнала максимум сигнала на выходе , где  — энергия входного сигнала .

По формулам (2.13) и (2.16) или (2.12) и (2.17) можно определить форму сигнала на выходе согласованного фильтра и для произвольного входного сигнала:

,                                    (2.19)

где

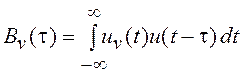                                   (2.20)

— взаимокорреляционная функция (ВКФ) произвольного входного сигнала  и сигнала , с которым фильтр согласован.

Спектр мощности шума (помехи) на выходе согласованного фильтра при воздействии на его вход белого шума со спектром мощности  может быть найден из (2.14) или из (2.10) и (2.15):

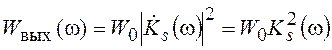.                      (2.21)

Отношение с/ш на выходе согласованного фильтра в момент  из (2.8), (2.18) и (2.21) определяется следующим образом:

(с/ш)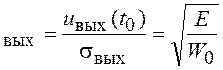,                             (2.22)

где

                                         (2.23)

— дисперсия шума на выходе фильтра.

Соотношение (2.22) подчеркивает тот замечательный факт, что максимальное значение отношения с/ш на выходе фильтра, согласованного с сигналом, определяется только энергией последнего и спектром мощности помехи и не зависит от формы этого сигнала.

3. ПОРЯДОК ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ

При выполнении курсовой работы предусмотрено использование ПК как для вычислений, так и для проведения математического моделирования и исследований в соответствии с индивидуальным заданием. С этой целью разработана прикладная программа FILTER, которая используется