Основные примеры статистической обработки результатов эксперимента

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

кафедра физики

Основные примеры статистической обработки результатов эксперимента

Основные сведения

СПб

2004

В пособии представлены варианты обработки прямых и косвенных измерений, а также обработка результатов измерений с помощью метода наименьших квадратов для конкретных физических измерений. Приводятся соответствующие алгоритмы вычисления. Пособие является дополнением к уже выпускавшимся на кафедре методическим разработкам по расчету погрешностей.

Основные приемы статической обработки результатов эксперимента

Под измерением понимают экспериментальное определение значения физической величины с помощью предназначенных для этого средств измерений (измерительных приборов). Измерение включает в себя наблюдение, т.е. собственно измерительную операцию и последующее выполнение математических операций по определению результата измерений.

Прямые измерения

Прямыми измерениями являются измерения, при которых с измерительного прибора непосредственно считывается измеряемая физическая величина. Погрешности, возникающие при измерениях, подразделяют на систематические погрешности и случайные погрешности. При этом, если систематическая погрешность заметно превышает случайную, то измерение проводят один раз; если погрешность, в основном, определяется случайными факторами, то измерения проводят несколько раз, чтобы после соответствующей статистической обработки результатов наблюдений случайная погрешность была меньше систематической. Серия независимых результатов, полученных в наблюдениях, называется выборкой.

Если дана выборка (x_i , i = 1…N), то ее статистическая обработка проводится следующим образом.

1.  Из результатов измерений исключаются обнаруженные систематические погрешности.

2.  Вычисляется выборочное среднее (среднее арифметическое) .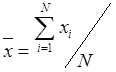

3.  Вычисляется выборочное среднеквадратическое отклонение (СКО) по формуле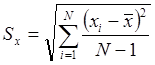  

4.  Вычисляется выборочное СКО среднего: .

5.  Задается доверительная вероятность P в диапазоне 0.9…0.99. Как правило, в примерах, приведенных в индивидуальных заданиях используется P = 0.95.

6.  Определяется доверительная случайная погрешность Dx = t_P,NS, где t_P,N – коэффициент Стьюдента. Значения коэффициентов Стьюдента табулированы. В индивидуальных заданиях использованы примеры выборок, состоящие из пяти наблюдений. Для таких выборок при P = 0.95 коэффициент Стьюдента t_95%, 5 =2.7.

7.  Определяется доверительная граница неисключенных систематических погрешностей. В индивидуальных заданиях достаточно учесть погрешность измерительного прибора , которую можно определить по классу точности прибора. Класс точности – число в кружке от 0.05 до 4 на шкале прибора означает систематическую погрешность от 0.05% до 4% максимального показания шкалы прибора. Грубые приборы не имеют класса точности, их погрешность принимается равной 0.5 цены наименьшего деления шкалы прибора.

8.   Рассчитывается полная доверительная погрешность результата измерения: .

9.  Вычисляется относительная погрешность dx = (Dx/)×100%.

10.  Округляются численные значения полной погрешности и результата измерения. Для этого сначала округляют погрешность до одной или двух значащих цифр. Две значащие цифры оставляют в случае, когда после округления до одной значащей цифры первая значащая цифра погрешности равна единице. (Так, 0.949 округляется до 0.9, а 0.951 – до 1.0). В остальных случаях оставляют одну значащую цифру. Результат округляется до того разряда, которым заканчиваются округленная погрешность. Если результат и погрешность не является окончательными, их не округляют.

11.Окончательный результат записывается в виде

.

12. Результаты расчетов сводятся в таблицу.

, =     ,         ,        ,

   ,      .

Косвенные измерения

Измерения называются косвенными, если их результат вычисляется по формулам, в которые подставляются результаты прямых измерений. Например, необходимо определить физическую величину f = f(x, y, z), являющуюся  функцией непосредственно измеренных величин x, y, z. При необходимости можно получить выборку косвенных измерений