Метод кинетического уравнения Больцмана

Лекция 11

Метод кинетического уравнения Больцмана

В исходном состоянии, электронный газ описывается статистикой Ферми-Диррака. Мы выделяем некоторую область, называемую поверхностью Ферми и говорим, что все состояния изнутри этой области заняты электронными состояниями. Но, кроме того, мы знаем, что электронный газ вырожденный. Не смотря на то, что у нас будет складываться внешнее воздействие, будет меняться только направление волнового вектора. Сохранение формы поверхности Ферми позволяет еще использовать так называемый метод электронной температуры. Пока внешнее воздействие g намного меньше функции распределения, может работать метод электронной температуры. Когда прикладывается внешнее воздействие, происходит перераспределение электронных состояний. Главная информация это скорость изменения функции распределения по состояниям.

Значит, у нас есть скорость изменения функции распределения по температуре за счет внешнего полевого воздействия (grad и gradT), коэффициент с вязанный с диффузией (grad(n)), и им будем пренебрегать, так как для металлов он практически не влияет (стремиться к 0), и коэффициент распределения направленного движения (импульса).  

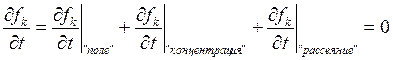
Полное число состояний, в любой системе, есть величина постоянная.

Кинетическое уравнение Больцмана:

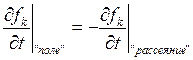
Метод кинетического уравнения Больцмана, это метод который позволяет анализировать кинетические свойства твердых тел в процессе переноса. При его решении мы можем найти время свободного пробега. 

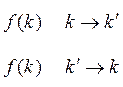
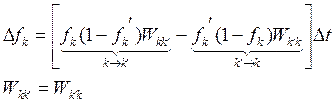
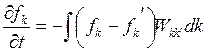
Процессы рассеяния связанные с потерей направленного движения они носят вероятностный характер. Результатом является нахождение времени, которое определяет скорость возвращение системы в исходное состояние. Это время называется временем релаксации.

Метод приближения времени релаксации

Этот метод основан на том, что мы считаем, что система линейная. Для всех систем существует метод малого сигнала.

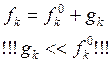
- возмущенная функция распределения по состояниям

-равновесная

-малая добавка

Скорость возврата системы в исходное состояние пропорциональна константе. Наша добавка убывает со скоростью 1/

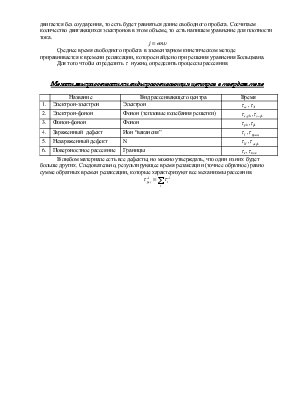
Теперь представим это графически

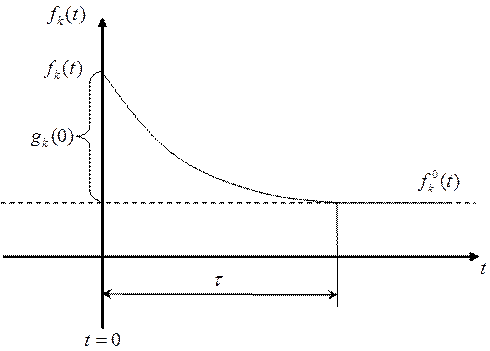Элементарный кинетический метод

Этот метод рассматривается для носителей электрического заряда и для носителей теплового. Результатом этого метода будет электропроводность 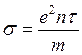, теплопроводность 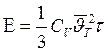. В чем же элементарность этого метода? Прежде всего, в нем используется модель свободного электронного газа. У нас вырожденный электронный газ. А так же . Будем рассматривать все процессы относительно одной частицы. У нас есть много электронов, все они могут находиться в любых состояниях К. При внешнем воздействии они переходят из одного состояния в другое и обратно. Можно все усреднить либо в какой то момент времени по все К состояниям, а можно представить что один электрон сначала последовательно находится в одном состоянии, потом во втором, третьем и так далее и усредним по времени. Из одного состояния в другое электрон переходит за счет потери направленного движения. При каждом акте взаимодействии с рассеивающим центром происходит потеря направленного движения.

Главные идеи метода:

1.  Рассматриваются электроны (фононы свободные частицы)

2.  Расчет ведется по отношению к одной частице движущейся в поле других

3.  Частица между соударениями двигается свободно

4.  При столкновении полностью теряет информация о направленности своего движения до столкновения ( теряет “память” )

5.  Теряет импульс, который был до столкновения

6.  Время соударения очень мало

7.  Соударения упругие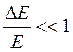

Направленное движение характеризуется импульсом. Выделим в нашем пространстве электронного газа некий объем, сечением S, такой, что между этими сечениями электрон двигается без соударения, то есть будет равняться длине свободного пробега. Сосчитаем количество двигающихся электронов в этом объеме, то есть напишем уравнение для плотности тока.

Среднее время свободного пробега в элементарном кинетическом методе приравнивается к времени релаксации, которое найдено при решения уравнения Больцмана.

Для того чтобы определить  нужно, определить процессы рассеяния.

Механизмы рассеивания и виды рассеивающих центров в твердом теле

В любом материале есть все дефекты, но можно утверждать, что один из них будет больше других. Следовательно, результирующее время релаксации (точнее обратное) равно сумме обратных времен релаксации, которые характеризуют все механизмы рассеяния.