Линейные пространства и линейная зависимость. Линейное нормированное пространство. Евклидово пространство. Действия с линейными операторами. Решение систем дифференциальных уравнений операционным методом

1.Линейные пространства (определение, примеры): Множество L называется линейным пространством, а его элементы векторами, если:

- задан закон, по которому любым двум элементам из множества L сопоставляется элемент z, принадлежащий L, и называется суммой x и y.

- задан закон умножения оператора на число, по которому элементу x из множества L и числу α, соотв. элем. y L, такой, что y= αx.

- для любых x,y и zL и любых чисел α,β выполняются следующие аксиомы  и :

1. x+y=y+x     2. (x+y)+z=x+(y+z)   3.  такой эл-т О (нулев. эл-т)

4. , , ((-х) – противоположный элемент)

5. α(x+y)= αx+ αy     6.( α+β)x= αx+βx       7. α(βx)=(αβ)x           8. x*1=x

Прим: 1) v- множество векторов на плоскости; v – линейное пространство

2)p – множество многочленов от 1ой переменной степени не выше 5; p -  линейное пространство.

2.Линейная зависимость (независимость) векторов: - вектора, принадлежащие L,  - вещественные числа.

Выражение вида называется линейной комбинацией векторов  с коэффициентами  .

Система векторов называется линейно зависимой, если существует равная О нетривиальная (невырожден. – хотя бы 1 из коэффициентов отличен от нуля) линейная комбинация этих векторов. В противоположном случае система называется линейно независимой.

Система векторов линейно зависима тогда, когда, по крайней мере, один из этих векторов является линейной комбинацией остальных.

Доказательство: 1. необходимо

Пусть  - линейно зависимая система векторов

Пусть    

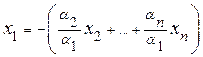
Следовательно,  линейная комбинация векторов.

2. Достаточно.

Пусть  (линейная комбинация векторов)

(-1)*

т.к., следовательно, система векторов линейно зависима.

Если в систему векторов входит нулевой вектор, то эта система будет линейно зависима.

Если какая-либо часть системы линейных векторов линейно зависима, то и вся эта система линейно зависима.

3. Базис. Координаты вектора. Размерность пространства. Система линейно независимых векторов  называется базисом пространства L, если любой вектор x из этого пространства может быть представлен в виде линейной комбинации этих векторов. 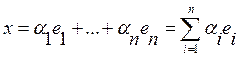  А числа  называются координатами вектора относительно данного базиса.  Если задан базис, то координаты вектора в данном базисе определены однозначно.

Доказательство:

Пусть  - базис. Предположим, что x разложен двумя способами.

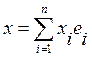
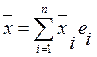
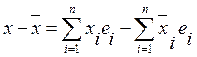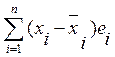==0

Т.к. линейная комбинация = 0, а вектора  линейно независимы =0, следовательно .

Пусть в линейном пространстве L выбран базис , тогда:

1)  при сложении векторов их координаты складываются.

2)  При умножении вектора на число его координаты умножаются на это число.

Доказательство: 1. xL, yL, , ,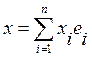

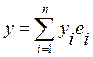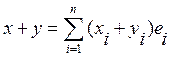
2. α – число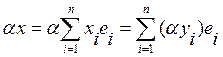

Если в линейном пространстве L существует базис из n векторов, то любой другой базис этого пространства так же содержит n векторов.

Линейное пространство L, в котором базис состоит из n векторов называется n-мерным, а число n  - размерностью пространства Lⁿ

4.Подпространство. Линейное нормированное пространство. Евклидово пространство. Непустое множество Z векторов в линейном пространстве L называется линейным подпространством, если для любых х и y принадлежащих Z: (x+y)=Z и для любого вектора xZ  α- число (αx) Z.

Множество называется линейным нормированным пространством, если для любого вектора х, принадлежащего этому множеству поставлено в соответствие вещественное число x - вещественное число, называемое нормой элемента х, причем выполняются следующие условия:

1. Если норма =0, то х=0.
2. Для любого числа αR или αС,  норма от произведения αх будет
3. Для любого элемента х, y, принадлежащего Н .

Линейное пространство называется евклидовым, если в этом пространстве определено скалярное произведение векторов. Каждому x и y поставлено в соответствие действительное число (x,y), причем выполняется следующее:

1. (x,y)=(y,x)              2. (λx,y)= λ(x,y)=(x, λy)                   3. (x₁+x₂,y)=(x₁,y)+(x₂,y)

4. (x,y)0                  5.  ()

Норма вектора x, равен  в евклидовом пространстве называется длиной вектора и обозначается =

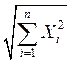
Вывод:

1. Если x и y принадлежат евклидовому пространству размерности n, тогда (x,y)=
2. x,y и ортогональны, если их скалярное произведение = 0 ((x,y)=0) и ,

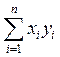
Система ненулевых векторов образует ортогональный базис в , если эти вектора попарно ортогональны, и ортонормальный базис, если каждый из векторов имеет длину =1.

5.Линейные операторы (определение, примеры). Пусть H и F – линейные пространства. Оператором A, действ. из H в F называется отображение вида A : Н  F. Сопост. любому  элементу

y=A(x)=Ax

Оператор А называется линейным, если для любых х₁,х₂  H , число.

1.

2.

Примечание:

1.А-умножается на число

 ,-число, x-вектор,

A-линейный оператор

2.      M ⁿ –линейное пространство,A-оператор дифференц.

-линейный оператор

6.Матрица линейного оператора. Образуется следующим образом:

матрица: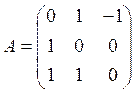

Пусть в заданном базисе  лин. простр.  каждому линейному опреатору А отвечает матрица , , тогда при сложении линейных операторов соответствующие им матрицы складываются, при умножении матрицы на число соответствующая матрица умножается на число, при умножении операторов