Линейные операторы и функционалы. Часть 2, страница 2

4.  Теорема о свертке.

Чрезвычайно важной операцией, выполняемой над функциями f(t) и g(t)является образование их свертки 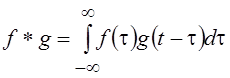, которую при фиксировании одной из функций можно рассматривать как линейный оператор.

Классическим примером свертки является отклик физически не реализуемой цепи с постоянными параметрами, имеющей импульсную характеристику h(t), на входной сигнал s(t): . Физическая нереализуемость означает, что импульсная характеристика h(t) отлична от нуля при t < 0. Напомним, что h(t) это реакция цепи на дельта-функцию, поданную на вход цепи в момент времени t = 0, т. е. для таких цепей отклик (следствие) возникает до подачи воздействия (причины).

Найдем преобразование Фурье свертки функций f(t) и g(t), что сводится к вычислению двойного интеграла вида 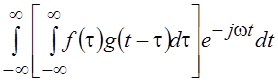. Меняя порядок интегрирования по t и t получим 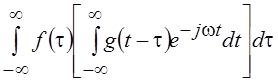. Выражение в квадратных скобках в соответствии с теоремой смещения есть . Учитывая, что 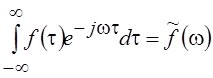, получим окончательно , т. е. свертке сигналов во временной области соответствует в частотной области перемножение спектров.

Аналогично доказывается, что произведению функций f(t)·g(t) соответствует свертка спектров  и , а именно  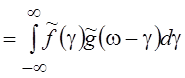. Наряду со спектром, задаваемым преобразованием Фурье сигнала s(t) для всей области его определения, иногда приходится рассматривать текущий спектр, который в зависимости от особенностей решаемой задачи может быть определен как

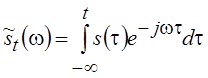                                         (5.6)

или

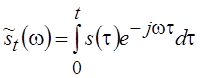.                                         (5.7)

Часто удобно использовать симметричную форму задания текущего спектра .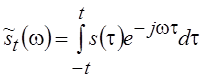

С помощью текущего спектра можно получить наглядную картину изменения спектра сигнала в зависимости от его длительности. Сделаем это для гармонического колебания s(t) = U_m cos w₀t, воспользовавшись симметричной формой задания текущего спектра:

.

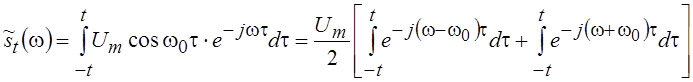При записи этого результата мы использовали известную форм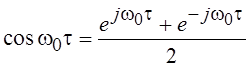улу Эйлера . Выполняя интегрирование и учитывая вторую формулу Эйлера 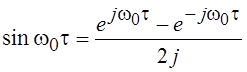, получим окончательно

 .

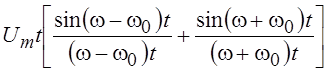Анализ этого выражения показывает, что при малых значениях t (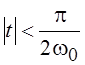) формируется спектр видеоимпульса, концентрирующийся вокруг нулевой частоты. С ростом t начинает формироваться спектр радиоимпульса, концентрирующийся вокруг частот ± w₀. При t ® ¥ мы получаем спектр гармонического колебания

,

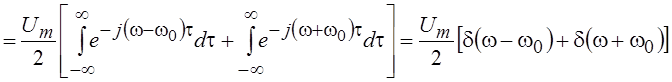представляющий собой две дельта-функции, расположенные в точках w₀ и –w₀. Такие спектры называют дискретными или линейчатыми.

Для синусоидального колебания s(t) = sin w₀t при задании текущего спектра в форме (5.7) получим:

.

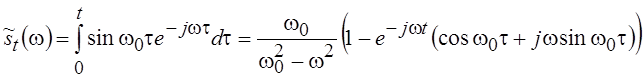Если рассматривать значения текущего спектра в дискретные моменты времени t = t_n = n = n, где Т₀ =  =  – период синусоидального колебания s(t), то можно получить выражение для амплитудно-частотного спектра в виде

.

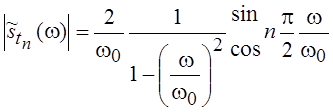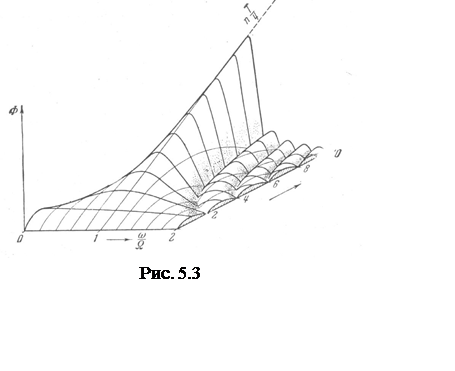Отметим, что п – это число полупериодов рассматриваемого колебания. В полученном выражении функция sin соответствует четным п, а cos – нечетным п.