Краткие сведения по теории функций комплексной переменной, страница 2

Интеграл от функции комплексного переменного задаётся как контурный интеграл вдоль некоторой ориентированной кривой C, на которой f(z) естественно полагается заданной: 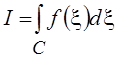, где буквой x обозначена комплексная переменная интегрирования.

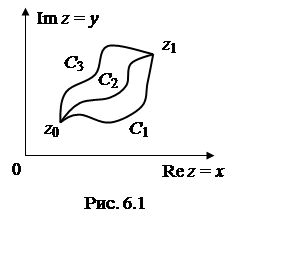
Большой интерес представляют интегралы от регулярных или аналитических функций. Если функция f(z) аналитична в области, в которой лежит контур C, то интеграл 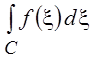 не зависит от пути интегрирования, а зависит лишь от начальной z₀ и конечной z₁ точек (см. рис.6.1). При этом естественно предполагается, что все рассматриваемые пути (С₁, С₂, С₃, …) не выходят за пределы области , в которой функция  f(z) аналитична. Следствием этого факта является теорема Коши. Если f(z) регулярна в замкнутой области  с границей C, то интеграл по замкнутому контуру C равен нулю:

.

Мощным аналитическим аппаратом является представление функций комплексного переменного с помощью степенных рядов. Справедлива следующая теорема.

Всякая функция f(z), аналитическая в кольце K, , может быть представлена в этом кольце своим рядом Лорана:

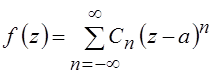.                                        (6.3)

Коэффициенты C_n вычисляются  по формуле

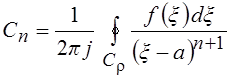,  n = 0, ±1, …                            (6.4)

где C_r – любой замкнутый контур, лежащий в кольце K и обходящий точку
z = a один раз в положительном направлении (против часовой стрелки). Структура ряда Лорана зависит от поведения функции в окрестности точки
z = a.

Если f(z) аналитична в точке z = a, т. е. аналитична в круге , то ряд Лорана превращается в ряд Тейлора, для которого C_n= 0  при n = –1,
–2, … . Если ряд (6.3) имеет вид

 ,

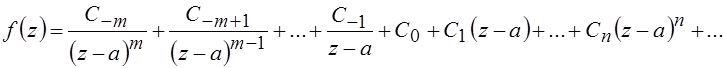то говорят, что функция f(z) имеет в точке  полюс порядка m.

Слагаемые 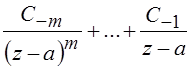 образуют главную часть ряда Лорана. Если главная часть ряда Лорана содержит бесконечное число членов, т. е. имеет вид

,

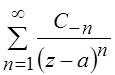то точка z = a является существенно особой точкой функции f(z).

Среди коэффициентов ряда Лорана наибольший интерес представляет C_-1, называемый вычетом функции f(z) в точке z = a. Как видно из (6.4),

,

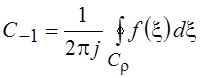т. е. интеграл по любому замкнутому контуру, охватывающему точку z = a и лежащему в кольце регулярности K равен . Обобщением этого факта является основная теорема о вычетах.

Пусть C₀ – простой замкнутый контур (это означает, что все точки контура проходятся один раз), внутри которого f(z) аналитична всюду за исключением конечного числа изолированных * особых точек а₁, а₂, а₃, …, а_п. Тогда

,

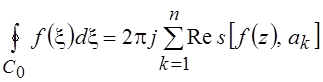где   – вычет функции f(z)  в точке z = a_k.

Рассмотрим вопрос об определении вычетов. Пусть f(z) имеет в точке
z = a полюс первого порядка, т. е.

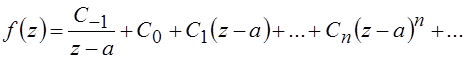.                   (6.5)

Умножая правую и левую части (6.5) на (z – a) и переходя к пределу при , получим: .

 Пусть f(z)  имеет в точке z = a полюс кратности m:

.

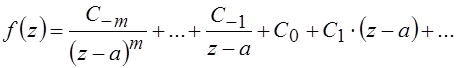Умножая правую и левую части на , дифференцируя (m – 1) раз по z и переходя затем к пределу при z ® 0, получим:

.

Вычисление большого числа несобственных интегралов базируется на лемме Жордана.

Если  и  при  по любому пути в верхней полуплоскости , и на действительной оси функция f(z)   аналитична, а в верхней полуплоскости имеет конечное число изолированных особых точек а₁, а₂, а₃, …, а_п, то

.

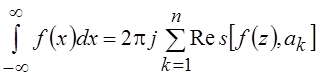Лемма Жордана может быть обобщена и на случай, когда функция f(z)    имеет на действительной оси конечное число полюсов первого порядка b₁, b₂, …, b_m. В этом случае выполняется равенство

.

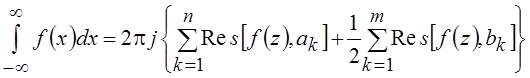Рассмотрим применение леммы Жордана для вычисления интеграла 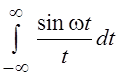, с которым мы столкнулись при изучении оператора Гильберта. Яcно, что от ω зависит лишь знак интеграла, а не его величина, так как, умножив и разделив на ω и сделав замену переменной, мы получим интеграл 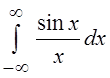. В то же время замена ω на –ω в силу нечётности синуса, меняет знак интеграла на противоположный. Применим лемму Жордана к функции 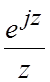 (, и условия леммы Жордана выполняются).

Интеграл

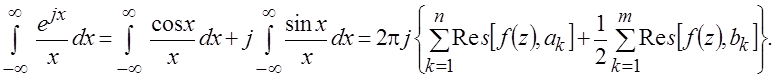
Функция 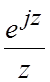 имеет единственную особую точку – полюс первого порядка в точке z = 0 и вычет 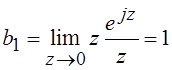. Таким образом,

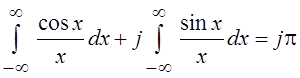
и по  условию равенства комплексных чисел

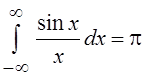, а .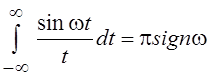

Завершим наш краткий экскурс в теорию функций комплексной переменной обсуждением понятия аналитического продолжения функции f(z).

Пусть однозначная функция f₁(z) определена и аналитична всюду в области D₁. Функция f₂(z), определённая и аналитическая в области D₂, является аналитическим продолжением функции f₁(z), если существует открытая область D₃, являющаяся пересечением областей D₁ и D₂, в которой функции f₁(z) и f₂(z)  совпадают.

Аналитическое продолжение f₂(z) определяется единственным образом по значениям f₁(z) в области D₃ и удовлетворяет каждому функциональному