Санкт-Петербургский государственный электротехнический университет
“ЛЭТИ”
ОТЧЕТ
по лабораторной работе по информатике № 2
Исследование сходимости бесконечного степенного ряда
Выполнил Евсеев О.Н.
Факультет РТ
Группа № 9192
Преподаватель Тупик В.А.
Выполнено “____” ___________
Подпись преподавателя __________
2009г.
Содержательная постановка задачи
Вычислить сумму первых К членов бесконечного степенного ряда
S=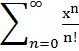
Вычисления заканчивать при таком К, что очередное
(следующее) слагаемое по модулю меньше некоторого наперед заданного числа ![]() (0<
(0<![]() <<1). Найти число
членов ряда.
<<1). Найти число
членов ряда.
Примечание: сумма ряда S при ![]() стремится
к функции
стремится
к функции ![]() .
.
Формальная постановка задачи
Дано: х, ![]() - действительные
числа
- действительные
числа
Найти: S – действительное, K – целое, где S=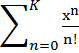 , K- число членов ряда.
, K- число членов ряда.
Программа заканчивает
вычисления, когда очередное слагаемое по модулю меньше ![]()
Тексты программ
1){$N+}
program abc;
uses crt;
var s,k,x,y,w,e,n,m:extended;
i:word;
begin
clrscr;
writeln('введите х');
read(x);
writeln('введите число эпсилон');
read(e); writeln;
w:=exp(x);
i:=1; s:=1;
writeln('exp в степени х - ',w);
n:=1; m:=1; y:=1;
k:=((x*y)/n);
if abs(k)>=e then
begin
repeat
s:=(s+k);
y:=(x*y);
m:=(m+1); n:=(n*m);
i:=(i+1);
k:=((x*y)/n);
until abs(k)<e;
end;
writeln('количество слогаемых - ',i);
writeln('сумма слогаемых s= ',s); writeln;
writeln('для выхода из программы нажмите любую клавишу');
readkey;
end.
2) {$N+}
program abc;
uses crt;
var x,k,s,e,w: extended;
i:longint;
begin
clrscr;
writeln('введите x');
read(x);
writeln('введите число эпсилон');
read(e);
w:=exp(x);
writeln('exp в степени х - ',w);
i:=1; s:=1; k:=1;
k:=k*(x/i);
if abs(k)>=e then
begin
repeat
s:=s+k;
i:=i+1;
k:=k*(x/i);
until abs(k)<e;
end;
writeln('количество слогаемых - ',i);
writeln('сумма слогаемых - ',s);
writeln('для выхода из программы нажмите любую клавишу');
readkey;
end.
Примеры расчета программ
|
X |
|
K |
|
S |
|
-0,1 |
0,01 |
2 |
9.04837418035960E-0001 |
9.00000000000000E-0001 |
|
0,1 |
0,01 |
2 |
1.10517091807565E+0000 |
1.10000000000000E-0000 |
|
-1,2 |
0,12 |
4 |
3.01194211912202E-0001 |
2.32000000000000E-0001 |
|
1,2 |
0,12 |
4 |
3.32011692273655E+0000 |
3.20800000000000E+0000 |
|
-9.1 |
0,001 |
29 |
1.11665808490115E-0004 |
6.73783856313822E-0004 |
|
9.1 |
0,001 |
29 |
8.95529270348251E+0003 |
8.95529165600254E+0003 |
Обе программы дают идентичные друг другу значения K и S.
Максимальное число X и K при ![]() =0.001:
=0.001:
|
X |
K |
|
|
1-ая программа |
644 |
1753 |
|
2-ая программа |
11356 |
30870 |
Вывод
Из примеров расчета следует, что точность расчетов обеих программ одинаковые. Из вычисления максимального числа членов ряда следует, что во второй программе ограничения вычислительных возможностей намного меньше, чем в первой.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.