





ИССЛЕДОВАНИЕ ГУН СВЧ
В данной работе исследуется СВЧ генератор, управляемый напряжением (ГУН). Такие автогенераторы (АГ) широко используются в синтезаторах частоты, анализаторах спектра, анализаторах цепей СВЧ и т.д.
1.1 Линейная теория автогенератора
Рассмотрим
активный элемент (транзистор, электронная лампа), три зажима которого соединены
комплексными проводимостями ![]() , как показано на рис.
1.
, как показано на рис.
1. 
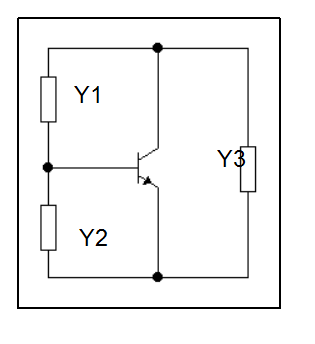 Будем
предполагать, что в эти проводимости входят также входные
Будем
предполагать, что в эти проводимости входят также входные ![]() , выходные
, выходные ![]() и
проходные
и
проходные ![]() проводимости активного элемента, за
исключением переходной проводимости (крутизны характеристики
проводимости активного элемента, за
исключением переходной проводимости (крутизны характеристики ![]() ), а также проводимости нагрузки
), а также проводимости нагрузки ![]() . В дальнейшем проводимости активного
элемента не учитываются и полагаются равными нулю. Кроме проводимостей
активного элемента в проводимости
. В дальнейшем проводимости активного
элемента не учитываются и полагаются равными нулю. Кроме проводимостей
активного элемента в проводимости ![]() входят внешние
(навесные) проводимости
входят внешние
(навесные) проводимости ![]() . Тогда выражения для
проводимостей будут иметь следующий вид:
. Тогда выражения для
проводимостей будут иметь следующий вид:
![]() . Суммарная проводимость их соединения
будет равна
. Суммарная проводимость их соединения
будет равна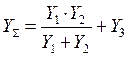 . На резонансной частоте
. На резонансной частоте ![]() мнимая часть
мнимая часть ![]() должна
обращаться в ноль. Будем полагать, что активный элемент включен как усилитель
напряжения (схемы с заземленным эмиттером, заземленным истоком, заземленным
катодом). Тогда напряжение на его входе
должна
обращаться в ноль. Будем полагать, что активный элемент включен как усилитель
напряжения (схемы с заземленным эмиттером, заземленным истоком, заземленным
катодом). Тогда напряжение на его входе ![]() (на
проводимости
(на
проводимости ![]() ) будет меньше чем выходное напряжение
) будет меньше чем выходное напряжение ![]() (на проводимости
(на проводимости ![]() ).
Соотношение между этими напряжениями определяется коэффициентом передачи цепи
).
Соотношение между этими напряжениями определяется коэффициентом передачи цепи ![]() и равно
и равно 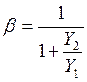 , где
, где ![]() - коэффициент обратной связи. Так как фаза
выходного напряжения усилителя повернута на 180˚ по отношению к входному, то
для обеспечения положительной обратной связи фазосдвигающая цепь
- коэффициент обратной связи. Так как фаза
выходного напряжения усилителя повернута на 180˚ по отношению к входному, то
для обеспечения положительной обратной связи фазосдвигающая цепь ![]() должна обеспечить такой же поворот фазы.
Следовательно коэффициент
должна обеспечить такой же поворот фазы.
Следовательно коэффициент ![]() должен быть
вещественным и отрицательным. Это означает, что
должен быть
вещественным и отрицательным. Это означает, что ![]() и
и ![]() должны иметь разные знаки и модуль
отношения
должны иметь разные знаки и модуль
отношения 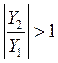 . Это возможно только, если мнимые
компоненты
. Это возможно только, если мнимые
компоненты ![]() и
и![]() -
- ![]() и
и ![]() имеют
разные знаки и
имеют
разные знаки и ![]() . Фазосдвигающая цепь резонирует
на частоте отличной от
. Фазосдвигающая цепь резонирует
на частоте отличной от ![]() . Для резонанса на частоте
. Для резонанса на частоте ![]() контур дополняется проводимостью
контур дополняется проводимостью ![]() , мнимая часть которой
, мнимая часть которой ![]() имеет тот же знак, что и
имеет тот же знак, что и ![]() , и величина
, и величина ![]() обеспечивает
выполнение равенства
обеспечивает
выполнение равенства 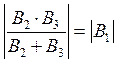 . На частоте резонанса
. На частоте резонанса 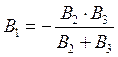 и тогда
и тогда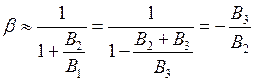 .
.
Такая
конфигурация схемы, когда активный элемент присоединен внешними выводами к
определенным точкам колебательного контура, носит название «трехточечной». В
диапазоне СВЧ чаще всего используется вариант «емкостной трехточки» (в
зарубежной литературе – «схема Колпица»), когда ![]() реализуется
в виде индуктивности, а
реализуется
в виде индуктивности, а ![]() в виде емкостей.
в виде емкостей.
Качество
работы автогенератора (АГ) в очень большой степени зависит от добротности его
колебательной системы. Если рассматривать колебательный контур, образованный
только навесными элементами ![]() , то его «собственная»
добротность
, то его «собственная»
добротность ![]() определяется главным образом добротностью
индуктивного звена, так как добротность емкостей заметно выше, чем добротность
индуктивностей. В схеме с активным элементом добротность уменьшается благодаря
активным компонентам проводимостей
определяется главным образом добротностью
индуктивного звена, так как добротность емкостей заметно выше, чем добротность
индуктивностей. В схеме с активным элементом добротность уменьшается благодаря
активным компонентам проводимостей ![]() . Такая добротность
называется «нагруженной» добротностью
. Такая добротность
называется «нагруженной» добротностью ![]() . По
определению добротность равна отношению энергии, запасаемой в реактивном
элементе контура на частоте резонанса (энергии, запасаемые в индуктивности или
емкости, одинаковы), к энергии, расходуемой на потери во всех элементах
контура.
. По
определению добротность равна отношению энергии, запасаемой в реактивном
элементе контура на частоте резонанса (энергии, запасаемые в индуктивности или
емкости, одинаковы), к энергии, расходуемой на потери во всех элементах
контура.
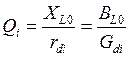 , здесь в числителях, соответственно,
реактивные сопротивление и проводимость индуктивности на частоте резонанса, в
знаменателях, соответственно, активные сопротивления и проводимости потерь в
контуре без активного элемента, пересчитанные к индуктивности. Выражение для
нагруженной добротности отличается тем, что в сопротивление и проводимость
потерь включены потери, связанные с активным элементом и нагрузкой. Определим
активные составляющие проводимостей
, здесь в числителях, соответственно,
реактивные сопротивление и проводимость индуктивности на частоте резонанса, в
знаменателях, соответственно, активные сопротивления и проводимости потерь в
контуре без активного элемента, пересчитанные к индуктивности. Выражение для
нагруженной добротности отличается тем, что в сопротивление и проводимость
потерь включены потери, связанные с активным элементом и нагрузкой. Определим
активные составляющие проводимостей ![]() .
. ![]() Ниже приведено выражения для проводимости
потерь
Ниже приведено выражения для проводимости
потерь ![]() , пересчитанной параллельно
, пересчитанной параллельно![]() в предположении, что
в предположении, что ![]() . Эти условия всегда выполняются для
высокодобротных контуров.
. Эти условия всегда выполняются для
высокодобротных контуров. 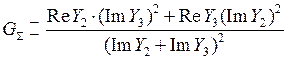 , тогда нагруженная
добротность будет равна
, тогда нагруженная
добротность будет равна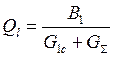 . Здесь
. Здесь ![]() - собственная проводимость потерь
индуктивности. Перейдем теперь к анализу работы АГ в линейном приближении.
- собственная проводимость потерь
индуктивности. Перейдем теперь к анализу работы АГ в линейном приближении.
Вольтамперные
характеристики (ВАХ) транзисторов (биполярных и полевых), а также таких
электронных ламп, как пентоды и тетроды, таковы (малая зависимость выходного
тока от напряжения питания), что их можно рассматривать как источники тока.
Тогда ток, протекающий через колебательный контур, будет равен:![]() , где
, где ![]() -
крутизна характеристики активного элемента по первой гармонике в области
рабочих токов АГ,
-
крутизна характеристики активного элемента по первой гармонике в области
рабочих токов АГ, ![]() - напряжение на входе активного
элемента, а
- напряжение на входе активного
элемента, а ![]() - напряжение на контуре (на проводимости
- напряжение на контуре (на проводимости ![]() ). Колебательный контур (КК) АГ состоит из
двух параллельно включенных цепей – цепи
). Колебательный контур (КК) АГ состоит из
двух параллельно включенных цепей – цепи ![]() и цепи
последовательно включенных
и цепи
последовательно включенных ![]() и
и ![]() . Для емкостной трехточки
. Для емкостной трехточки ![]() есть индуктивность, а
есть индуктивность, а ![]() - емкости. Проводимость цепочки
- емкости. Проводимость цепочки ![]() равна
равна 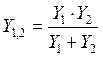 . В
предположении высокой добротности КК приближенное значение этой проводимости
будет равно:
. В
предположении высокой добротности КК приближенное значение этой проводимости
будет равно: ![]()
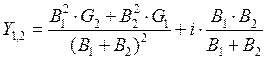 . Так как ранее все
активные проводимости были перечислены к
. Так как ранее все
активные проводимости были перечислены к ![]() , то
, то ![]() можно положить равным нулю и тогда
можно положить равным нулю и тогда 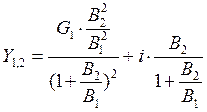 . Ранее было показано, что коэффициент
обратной связи равен
. Ранее было показано, что коэффициент
обратной связи равен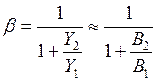 . Тогда
. Тогда 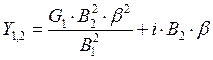 .
Из выражения для
.
Из выражения для ![]() следует, что
следует, что 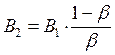 , тогда
, тогда ![]() .
Активная проводимость
.
Активная проводимость ![]() включает в себя все потери КК и
поэтому
включает в себя все потери КК и
поэтому 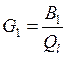 . Следовательно, окончательно
. Следовательно, окончательно 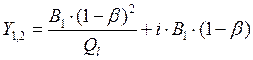 . Памятуя о том, что для обеспечения положительной
обратной связи, значение
. Памятуя о том, что для обеспечения положительной
обратной связи, значение ![]() должно быть вещественным
и отрицательным,
должно быть вещественным
и отрицательным, 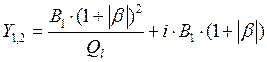 . Следовательно, КК может быть
представлен в виде параллельного соединения трех проводимостей: активной
. Следовательно, КК может быть
представлен в виде параллельного соединения трех проводимостей: активной 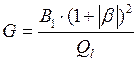 , индуктивной
, индуктивной ![]() и
емкостной
и
емкостной ![]() . Теперь удобно перейти от проводимостей к сопротивлениям:
активное сопротивление
. Теперь удобно перейти от проводимостей к сопротивлениям:
активное сопротивление 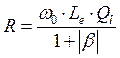 , индуктивное
, индуктивное ![]() , где
, где 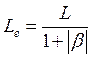 и
емкостное
и
емкостное 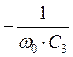 (рис.2). Все эти сопротивления соединены
параллельно и через них текут токи:
(рис.2). Все эти сопротивления соединены
параллельно и через них текут токи: 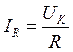 ,
, 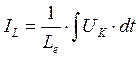 и
и 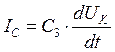 .
Сумма этих токов должна быть равна току
.
Сумма этих токов должна быть равна току ![]() ,
который создается активным элементом
,
который создается активным элементом . Продифференцировав
это уравнение по времени, получаем дифференциальное уравнение следующего вида:
. Продифференцировав
это уравнение по времени, получаем дифференциальное уравнение следующего вида:
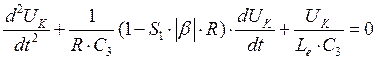 . Решением этого уравнения будет:
. Решением этого уравнения будет: 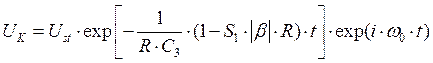 , где
, где ![]() - стационарная
(установившаяся при выполнении «баланса амплитуд») амплитуда колебаний. Самовозбуждение
АГ может произойти, только если выполняется условие
- стационарная
(установившаяся при выполнении «баланса амплитуд») амплитуда колебаний. Самовозбуждение
АГ может произойти, только если выполняется условие ![]() .
Подставим в это выражение представление
.
Подставим в это выражение представление 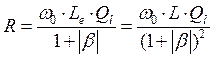 и
получим условие
и
получим условие 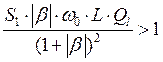 . В этом выражении крутизна
. В этом выражении крутизна 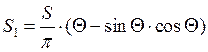 , где
, где ![]() есть
статическая крутизна активного элемента в выбранной рабочей точке, а
есть
статическая крутизна активного элемента в выбранной рабочей точке, а ![]() - угол отсечки. По мере роста амплитуды
напряжения
- угол отсечки. По мере роста амплитуды
напряжения ![]() на контуре, крутизна уменьшается благодаря
уменьшению угла отсечки, в конце концов, неравенство становится равенством, и
АГ переходит в стационарный режим работы – выполняется условие «баланса
амплитуд». Значение угла отсечки при этом определяется из уравнения
на контуре, крутизна уменьшается благодаря
уменьшению угла отсечки, в конце концов, неравенство становится равенством, и
АГ переходит в стационарный режим работы – выполняется условие «баланса
амплитуд». Значение угла отсечки при этом определяется из уравнения 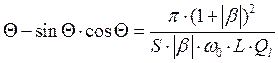 . Нагруженную добротность
. Нагруженную добротность ![]() желательно иметь порядка половины собственной
добротности
желательно иметь порядка половины собственной
добротности ![]() КК АГ [1]. Большое значение
КК АГ [1]. Большое значение ![]() требует слабой связи транзистора с КК,
т.е. малого значения
требует слабой связи транзистора с КК,
т.е. малого значения ![]() , а это, в свою очередь требует,
чтобы
, а это, в свою очередь требует,
чтобы ![]() было бы значительно меньше
было бы значительно меньше ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.