Исследование искажений сигналов на выходе фильтра нижних частот

СПбГЭТУ

Кафедра ТОЭ

Пояснительная записка к курсовой работе

«исследование искажений сигналов на выходе фильтра нижних частот»

Преподаватель Чернышев Э.П. 

Студент гр. 2351               

Санкт-Петербург

2004г.

Содержание

1.  Техническое задание.........................................................................................................2

2.  Нормировка........................................................................................................................3

3.  Расчет передаточной функции цепи................................................................................3

4.  Расчет частотных характеристик цепи............................................................................4

5.  Составление уравнений состояния цепи.........................................................................5

6.  Определение переходной и импульсной характеристик................................................8

7.  Вычисление реакции цепи при воздействии одиночного импульса на входе.............12

8.  Определение спектральных характеристик одиночного импульса воздействия........15

9.  Вычисление спектра реакции при одиночном импульсе на входе...............................17

10.  Определение спектра периодического входного сигнала..............................................19

11.  Приближенный расчет реакции при периодическом воздействии...............................22

12.  Выводы................................................................................................................................24

13.  Список литературы.............................................................................................................25

1.  Техническое задание

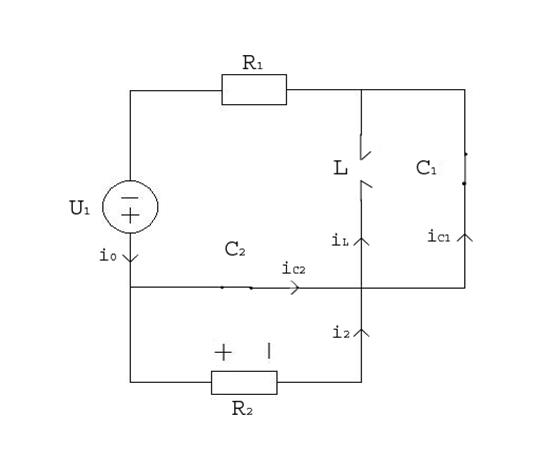
На вход электрической цепи (рисунок 1) с момента t=0 подается импульс напряжения U₁. Реакцией цепи является напряжение U₂= U_R2. График импульса представлен на рисунке 2, данные схемы и импульса представлены в таблице 1.

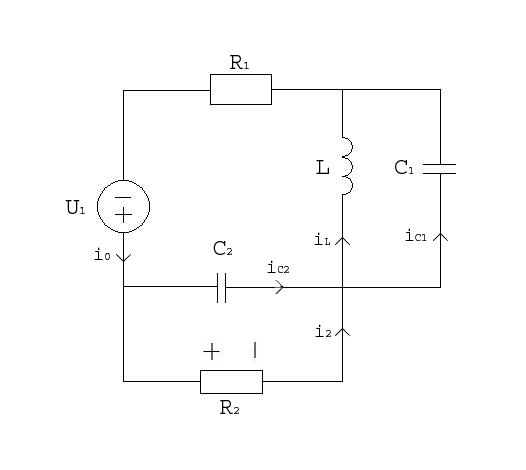
Рисунок 1. Схема

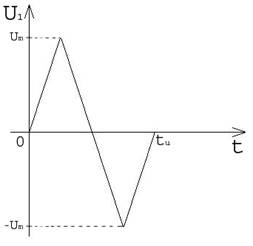
Рисунок 2. Входной импульс

Таблица 1. Данные схемы

R1=R2, кОм	L1, мГн	С1, пкФ	С2, пкФ
0,9	0,8	555	1000

Таблица 2. Данные импульса

Um, В	tи, мкс
100	12,56

2.  Нормировка

Проведем нормировку параметров цепи используя R_б=R₁=R₂=900 Ом и w_б=10⁶ с^-1:

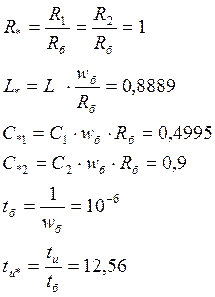
в дальнейшем индекс «*» будет опущен.

3.  Расчет передаточной функции цепи

Для определения передаточной функции цепи используем метод пропорциональных величин. Пусть выходная реакция = 1.

Z_L=0,9S

Z_C1=2/S

Z_C2=1/(0,9*S)

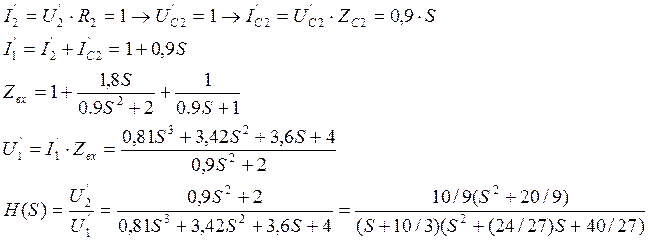
Нули передаточной функции:      S_01,02= ±j1,49

Полюса передаточной функции:  S₁= -3,333; S_1,2= -0,445±j1,14

Их расположение на комплексной плоскости – рисунок3.

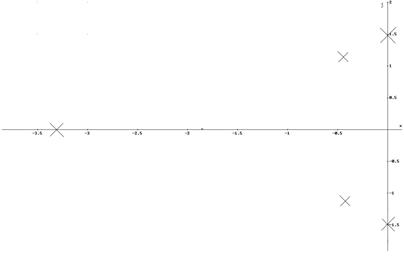
Рисунок 3. Расположение нулей и полюсов на комплексной плоскости

Время практической длительности переходных процессов: t_пп=3τ_max+π/2=-3/S_min+ π /2=8,29

4.  Расчет частотных характеристик цепи

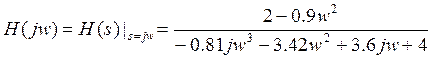                                                       (4.1)

Амплитудно-частотная характеристика:

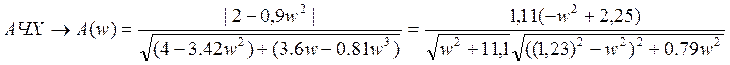 (4.2)

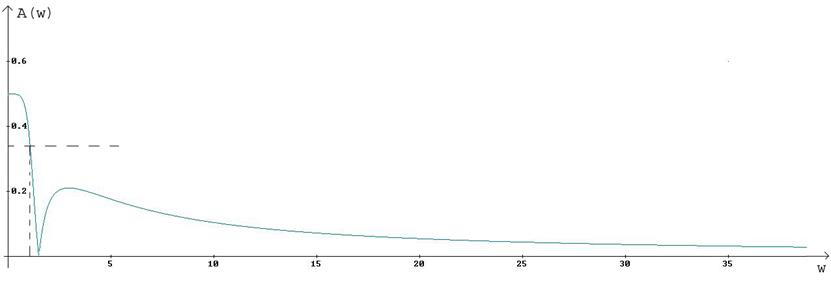
Рисунок 4. АЧХ

А(0)=0,5                                                                                                                               (4.3)

Из рисунка 4 видно, что полосу пропускания цепи составляют частоты от 0 до 1. Из 4.3 видно, что амплитуда выходного сигнала составит половину от амплитуды входного.

Фазо-частотная характеристика

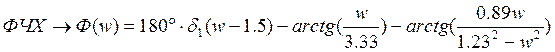                               (4.4)

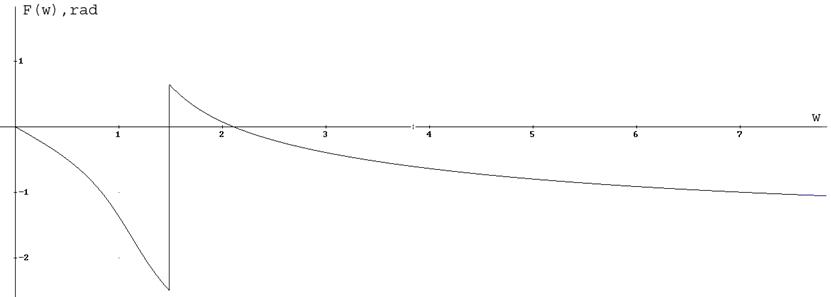
Рисунок 5. ФЧХ

Время запаздывания t_з=Ф(0)’=0.9

Амплитудно-фазовая характеристика. Её график на рисунке 6.

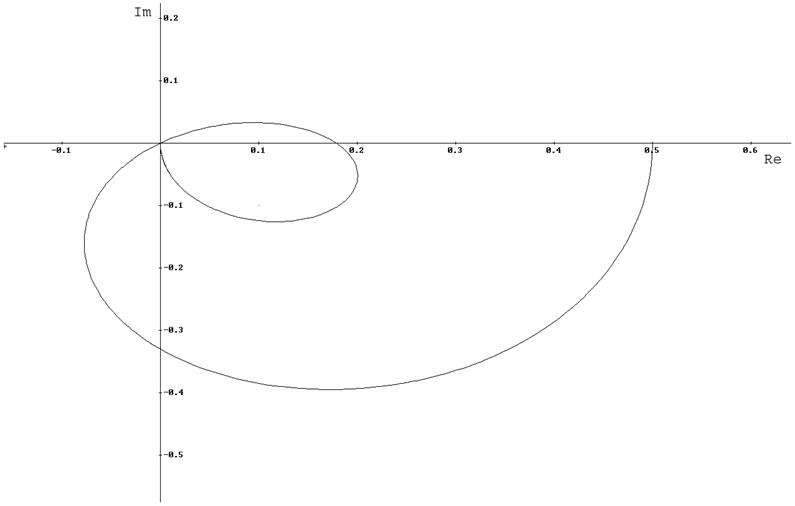
Рисунок 6. АФХ

5.  Составление уравнений состояния цепи

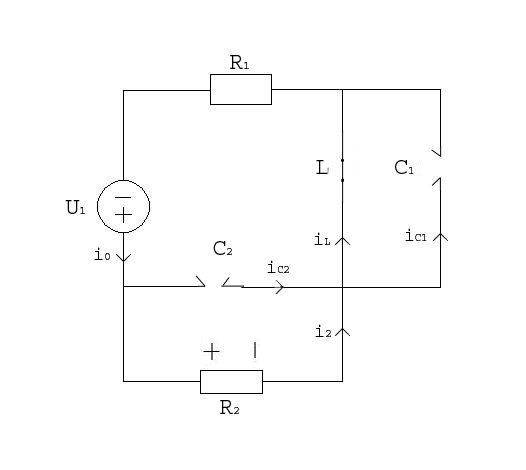
Заменяем L-элемент на ИТ, а С-элементы на ИН. Получим схему замещения, показанную на рисунке 7.

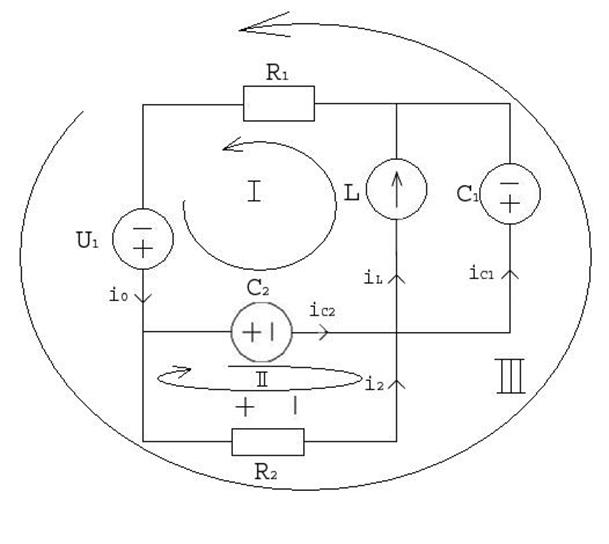
Рисунок 7. Схема замещения

В полученной резистивной цепи методом контурных токов найдем  U_L, i_C1, i_C2.

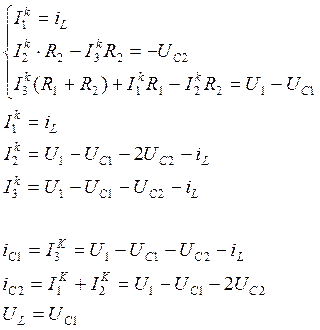
Используя соотношения  U_L=Li_L’; i_C=CU_C’ получим уравнения состояния:

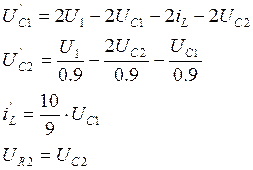
Уравнения состояния в матричной форме:

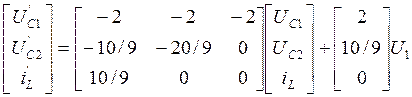
ХП: det[(A)-p(E)]=0

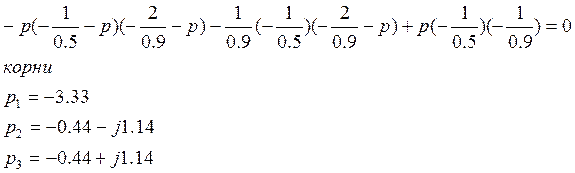
Контроль уравнений состояния:

U₁=б₁(t)

t=0+

i_C1=i_C2=U₁/R₁=1  è U_C1’=i_C1/C₁=1/C₁

                                  U_C2’=i_C2/C₂=1/C₂

U_L=0 è i_L’=0

                                  i_L’(0+)=0

Такие же значения получаем из уравнений состояния при t=0+

i_L’(0+)=0  U_C1’(0+)=1/R₁C₁     U_C2’(0+)=1/R₁C₂

tè∞

i_L=U₁/(R₁+R₂)=0.5   U_C1=0   U_C2=i_LR₂=0.5          i_L(∞)=0.5   U_C1(∞)=0   U_C2(∞)=0.5

Такие же значения получаем из уравнений состояния, приравняв левую их часть к нулю

i_L=0.5   U_C1=0   U_C2=i_LR₂=0.5

6.  Определение импульсной и переходной характеристики

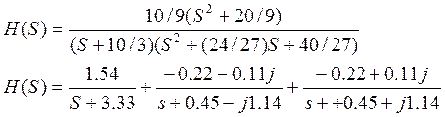
Импульсная характеристика – оригинал H(S):

h(t)=1.54e^-3.33t+(-0.22-0.11j)e^{-(0.45-1.14j)t}+(-0.22+0.11j)e^{-(0.45+1.14j)t}

h(t)=1.54e^-3.33t-0.426e^-0.45tcos(1.14t)+0.21e^-0.45tsin(1.14t)

h(t)=1.54e^-3.33t-0.475e^-0.45tcos(1.14t-2.682)

Изображение переходной характеристики

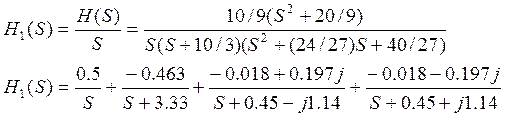
Переходная характеристика:

h₁(t)=0.5-0.463e^-3.33t+(-0.018-0.197j)e^{-(0.45-1.14j)t}+(-0.018+0.197j)e^{-(0.45+1.14j)t}

h₁(t)=0.5-0.463e^-3.33t-0.0344e^-0.45tcos(1.14t)+0.385e^-0.45tsin(1.14t)

h₁(t)=0.5-0.463e^-3.33t-0.386e^-0.45tcos(1.14t+1.66)

Контроль

h₁(∞)=0.5

h₁(0+)=[0.5-0.463e^-3.33t-0.386e^-0.45tcos(1.14t+1.66)]_t=0+=0

Используя теоремы о конечном и начальном значениях:

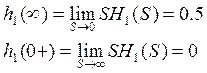
Значения совпадают è верно

График импульсной характеристики и переходной характеристики, полученных аналитическим методом

h(t)=1.54e^-3.33t-0.475e^-0.45tcos(1.14t-2.682)

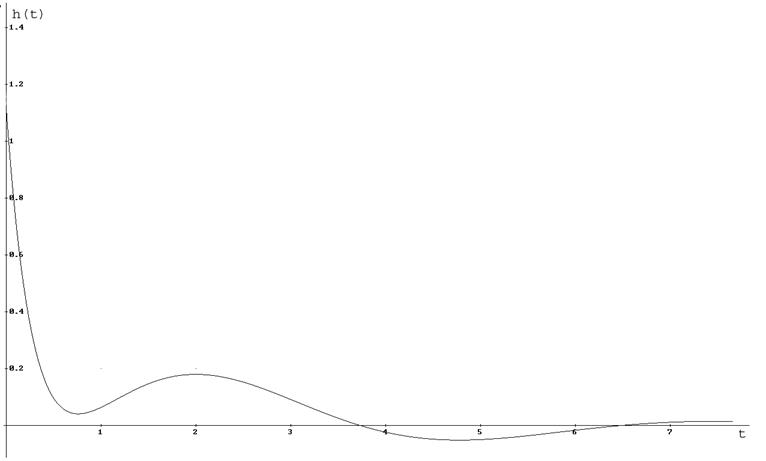
Рисунок 8. h(t)

h₁(t)=0.5-0.463e^-3.33t-0.386e^-0.45tcos(1.14t+1.66)

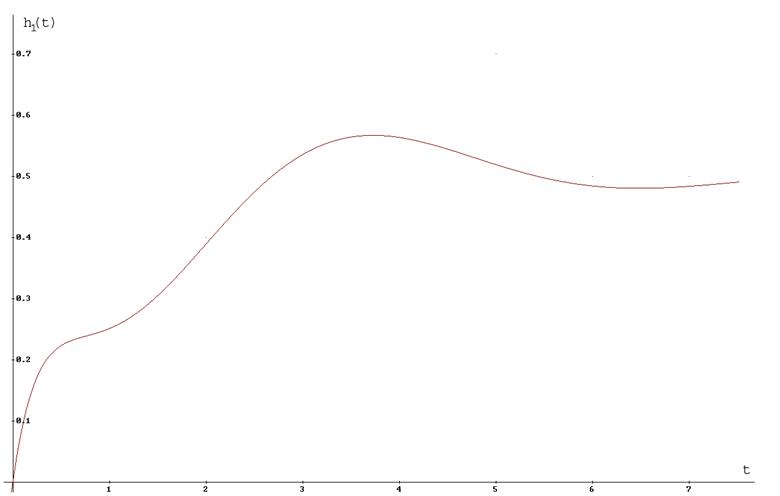
Рисунок 9. h₁(t)

Численный метод расчета переходной характеристики:

В п.5 курсовой работы получили следующие уравнения состояния:

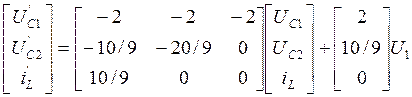
Выберем шаг дискретности ∆t=0.05 при τ₁=0,67с и τ₂=2,24с

Алгоритм Эйлера в данном случае:

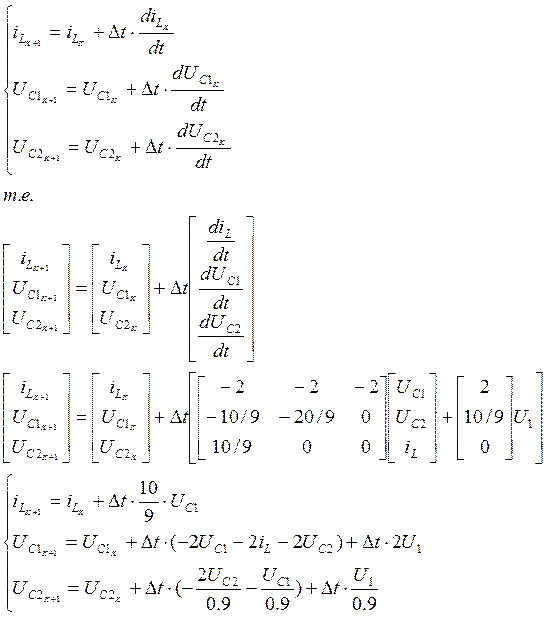
Выбрали шаг дискретности ∆t=0.05 таким образом, что минимальной постоянной времени τ₁=0,67 соответствовало15 шагов расчета. Практическое время переходного процесса t_пп=6,72

График переходной характеристики, полученной численным методом:

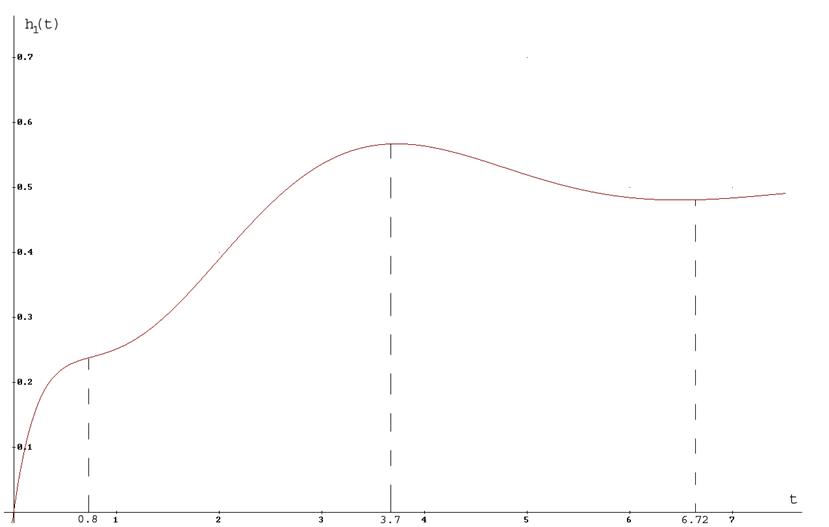
Рисунок 10.  h₁(t) численный метод

Оценка точности численного расчета (по характерным точкам)

Точки	Аналитический	Численный
t1=0.8	0.2409	0,2339
t2=3.7	0.5671	0,5801
t3=6.72	0.4813	0,4765
t4=9.2	0.5056	0.5083
t5=0+	0	0
t6=∞	0.5	0.4765

Вывод: численный расчет показал довольно точные значения переходной характеристики

7.  Вычисление реакции на воздействие одиночного импульса

аналитическим методом.

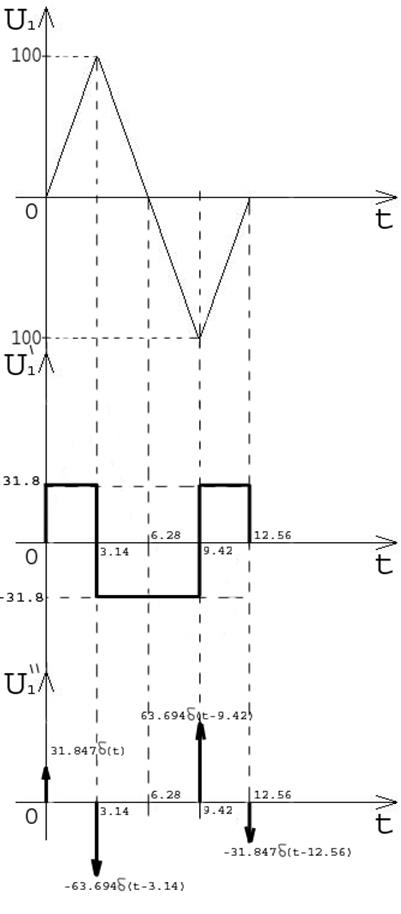
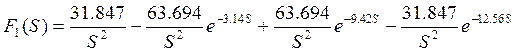
Изображение по Лапласу входного сигнала

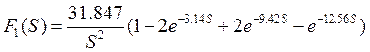
Передаточная функция цепи:

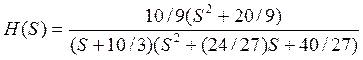
Изображение по Лапласу выходного сигнала:

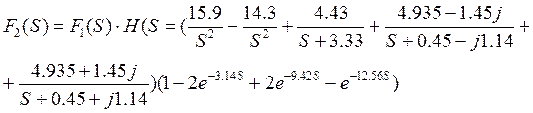
Выходной импульс:

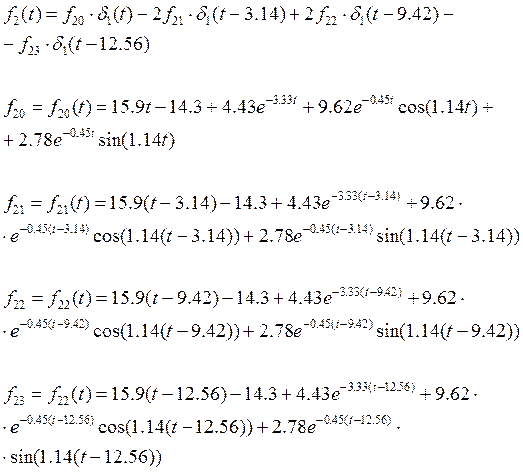Итак:

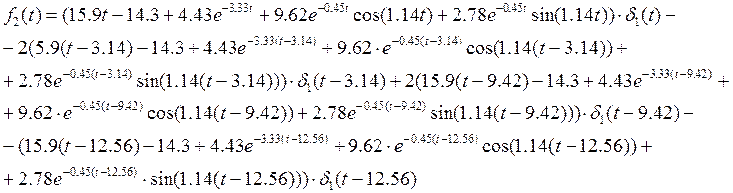
График реакции цепи на воздействие одиночного импульса (аналитический метод)

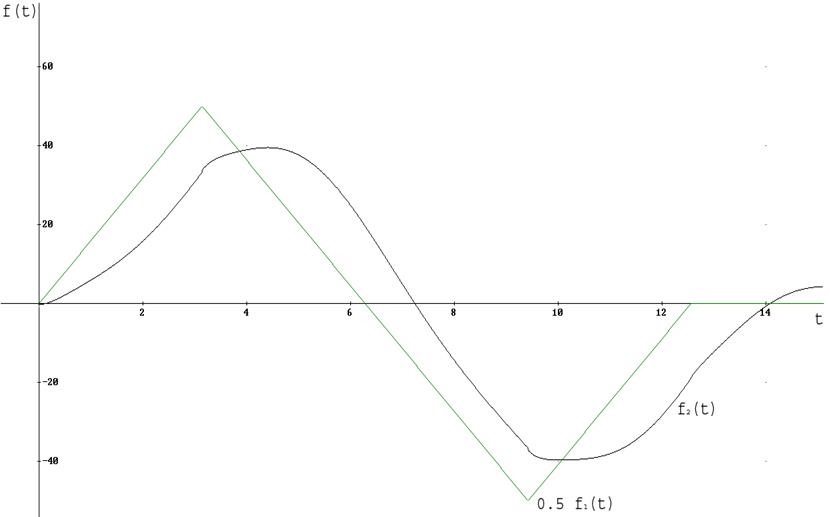
Рисунок 11. график f₂(t)

Выводы относительно правомерности оценок, сделанных в п.4:

Цепь реализует операцию  f_вых(t)=k*f_вх(t-t_з)

По графику видно, что сигнал прошел на выход с незначительными искажениями.

Коэффициент k и время запаздывания t_з определим по графику

k=43.8/100=0.438

t_з=7.2-6.28=0.92

Сравнивая значения k и t_з с ранее полученными в п.3 делаем вывод: оценки k и t_з произведены довольно точно.

Численный метод расчета реакции цепи на воздействие одиночным импульсом

При выполнении численного расчета переходной характеристики в п.6 было получено

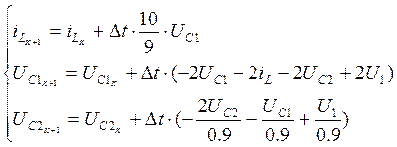
Воздействие одиночного импульса можно представить в виде:

U₁(t)=31.847δ₁(t)-63.694 tδ₁(t-3.14)+200 δ₁(t-3.14)+63.7t δ₁(t-9.42)-600 δ₁(t-9.42)-

-31.847t δ₁(t-12.56)+400 δ₁(t-12.56)

Шаг дискретности ∆t=0.05, которому соответствует 15 шагов расчета. При этом время переходного процесса: t_пп=3τ_max+π/2=-3/S_min+ π /2=8,29

График реакции, полученной численным методом расчета 

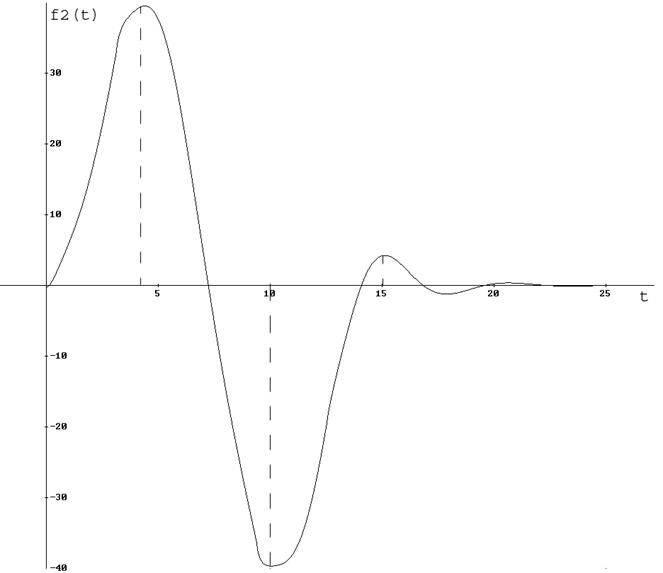
Рисунок 12. График f₂(t)

Оценка точности численного расчета (по характерным точкам):

Точки	Аналитический	Численный
t1=4.324	39.139	39,235
t2=10	-39.118	-39,25
t3=15.2	4.249	4,958
t5=0+	0	0
t6=∞	0	-0.032

Вывод: численный расчет показал довольно точные значения реакции цепи на воздействие одиночным импульсом

8. Определение спектральных характеристик одиночного импульса воздействия

Изображение одиночного импульса по Лапласу

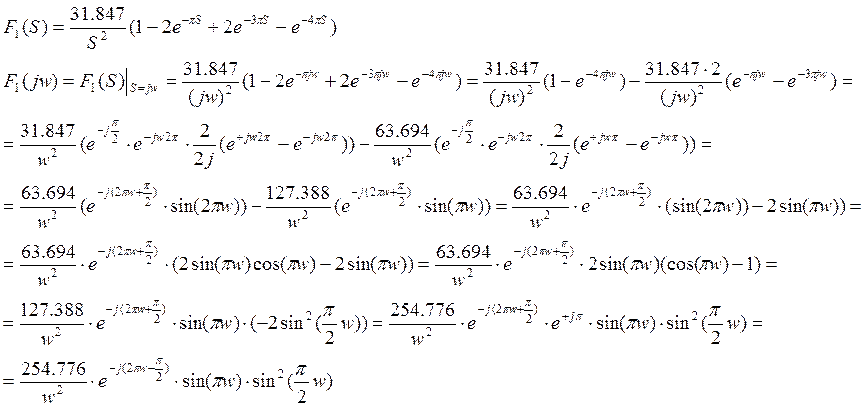
Амплитудный спектр: А₁(w)=|F₁(jw)|=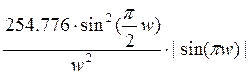 

Фазовый спектр Ф₁(w)=arg(F₁(jw))=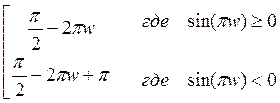

Проверка: S_вх=100*6,28*0,5-100*(12,56-6,28)*0,5=0

                  F₁(j0)= S_вх =0

Определим ширину спектра по 10% амплитудному критерию:

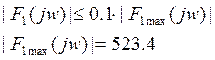è∆w=1.5146

Вывод: спектр входного сигнала практически полностью укладывается в полосу пропускания цепи и следовательно искажения сигнала по форме на выходе цепи будут