Исследование движения микрочастиц в потенциальных полях

Санкт-Петербургский государственный электротехнический университет

“ЛЭТИ”

                                       ОТЧЕТ

по лабораторной работе № 2

     Исследование движения микрочастиц в потенциальных полях

Выполнил    Заболовский В.С.      

                        Факультет РТ

                        Группа № 2191

Преподаватель 

“Выполнено”  11.10.2013

Подпись преподавателя __________

ЦЕЛЬ РАБОТЫ: ознакомление с методикой и особенностями решения квантово - механических задач для простейших случаев.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ:

Законы квантовой механики составляют основную теоретическую базу в изучении строения вещества. Так, опираясь на них, удалось выяснить строение атомов, установить природу химической связи, объяснить периодическую систему элементов, понять строение атомных ядер и свойства элементарных частиц.

Описание движения частиц в одномерном случае

Уравнение, решения которого определяют движение микрочастицы, запишется:

 (x,t) - волновая функция, описывающая состояние микрочастицы;

m, кг - ее масса;

h  -   постоянная Планка;

U(x,t) - потенциал силового поля, действующего на частицу.

В случае постоянства потенциала решение уравнения (1) имеет вид волн де-Бройля.

где импульс частицы:

Низкий потенциальный скачок ( см. Рисунок 1).

В этом случае энергия частицы больше высоты потенциального скачка (E>U).

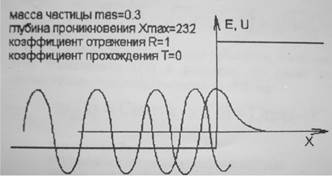
Рисунок1 - Решение уравнения Шредингера для случая высокой потенциальной ступеньки

Для стационарного случая (независимости физической ситуации от времени) решение уравнения Шредингера

в соответствии с выражением (2) будет представлено для области слева от х=0 суммой падающей волны и отраженной:

Здесь в отсутствие силового поля в первой области (U=0) согласно (3)

В области справа от x=0 решение будет представлено амплитудой прошедшей волны:

Где

Для того, чтобы задача имела конкретно завершенный вид и имела четкий физический смысл, необходимо в решениях (5-6) найти неопределенные коэффициенты А, В и С. Для нахождения этих коэффициентов используют аксиоматические свойства волновой функции  (x):

-  непрерывность самой функции и ее производных;

-  однозначность волновой функции;

-  ее ограниченность.

Эта процедура называется "сшиванием” волновой функции на границе скачка потенциала.

Во-первых, нужно приравнять значения волновых функций слева и справа от точки х=0

что дает:

Далее необходимо найти первые производные по х от  и также приравнять их друг другу в точке х=0

что должно привести к выражению:

Система (7-8) легко приводит к решению для коэффициента С:

Физический смысл этого выражения достаточно понятен - оно выражает амплитуду прошедшей волны С через амплитуду падающей А. Соответственно, для коэффициента В будем иметь:

Здесь амплитуда отраженной волны В выражена через амплитуду падающей волны А.

Далее легко найти коэффициент отражения R на прямоугольном потенциале, как отношение интенсивностей отраженной и падающей волн или, соответственно, по статистическому смыслу волновой функции, как отношение квадратов амплитуд этих волн. Тогда из соотношения (10) будем иметь:

Из закона сохранения числа частиц легко получить коэффициент проз­рачности потенциальной ступени, если понимать под ним долю потока частиц, прошедших вправо от границы.

Высокий потенциальный скачок (E<U).

В классическом случае закон сохранения энергии не позволяет ни одной классической частице оказаться в области, где бы ее потенциальная энергия стала больше первоначальной кинетической. Поэтому все они до одной должны отражаться на границе х=0.

Методика решения задачи в этом случае включает следующие этапы:

1)  по-прежнему, область пространственной координаты разбивается на две части и в области до границы раздела, т.е. при х<0 уравнение Шредингера (4) остается таким же с U=0, поэтому такими же остаются и решения (5)

2)  серьезным изменениям подвергается уравнение Шредингера для области высокого потенциала (х>0). Здесь (E-U)<0 и второе слагаемое уравнения (4) меняет знак. Однако, если сделать следующую замену обозначений в выражении (6а);

С тем, чтобы сохранить и форму уравнения и его решение прежним, то после этой подстановки (14) в решение (5) получим окончательное решение в виде суммы теперь уже вещественных экспонент:

С тем, чтобы удовлетворить свойству конечности волновой функции на бесконечности, очевидно коэффициент С в решении (13) необходимо выбрать равным нулю:

С=0

3)   для определения оставшихся произвольных постоянных А, В и D снова нужно использовать свойство непрерывности волновых функций, т. с. опять провести операцию «сшивания»:

После корректно проведенной операции можно получить выражения для амплитуд волны падающей А и отраженной В:

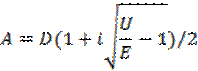
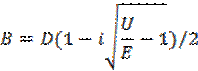
Коэффициент  отражения,  как отношение интенсивностей отраженной волны В и падающей волны А запишется в виде равенства:

 Прямоугольный потенциальный барьер

Силовое поле, представленное на Рисунке 2, называется потенциальным барьером высоты U₀ и ширины L.

Рассмотрим задачу о движении частицы слева и падении ее на барьер.

 Пусть барьер будет высоким: энергия Е частицы меньше высоты барьера Е<U₀.

Как утверждает макроскопический опыт, поток частиц в этом случае должен полностью отражаться.