Исследование движения микрочастиц в потенциальных полях, страница 2

область пространственной координаты разбивается на три части:

1)  до границы раздела, где -∞< X< 0   уравнение Шредингера (4) остается таким же с U=0, поэтому такими же остаются и решения (5)

(17)

2)  для области высокого потенциала  0<X<L, где (E-U)<0, в уравнении Шредингера второе слагаемое снова меняет знак. И если сделать уже знакомую замену обозначений в выражении (6а):

(18)

С тем, чтобы сохранить и форму уравнения, и его решение прежним, то после этой подстановки (18) в решение (5) снова получим решение в виде суммы теперь уже вещественных экспонент:

(19)

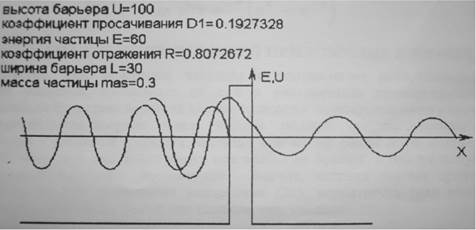
Рисунок 2 - Решение уравнения Шредингера для потенциального барьера конечной ширины

3)  справа от барьера, где х>L, частиц, идущих к барьеру нет, там могут быть только частицы, идущие со стороны барьера вправо. Волновая функция в этой области, как решение уравнения должна быть следующей:

(20)

Для определения произвольных постоянных А, В, С, D и F снова нужно использовать свойство непрерывности волновых функций, т.е. опять провести операцию «сшивания» на границе х=0:

и на границе x=L:

Используя выражения для волновой функции (17), (19) и (20), можно подучить выражения для амплитуд волны падающей А и отраженной В, выраженных через амплитуду волны прошедшей F:

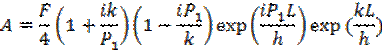
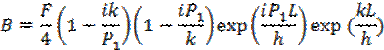
Самой интересной особенностью решения этой задачи является возможность найти отношение интенсивности прошедшей волны F к интенсивности падающей А, т.е. коэффициент прозрачности (проницае­мости) D1

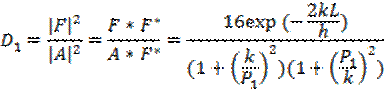
коэффициента прозрачности D1 уже легко получить выражение через энергии: здесь F^* и А^* соответствующие комплексно сопряженные величины.

Отсюда для

(21)

Можно показать, что коэффициент отражения, как отношение ин­тенсивности отраженной волны В к интенсивности падающей А, сводится к следующему выражению:

(22)

где shx=(e^x-e^-x)

ВЫПОЛНЕНИЕ РАБОТЫ И ОБРАБОТКА РЕЗУЛЬТАТОВ

I).  Зависимость коэффициента  отражения  (R) от варьирования энергии частицы (E) при постоянных значениях высоты потенциала (U) и массы частицы; как в  области E>U ,так и для U >E.

E>U

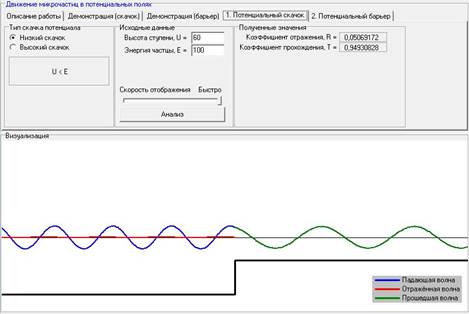
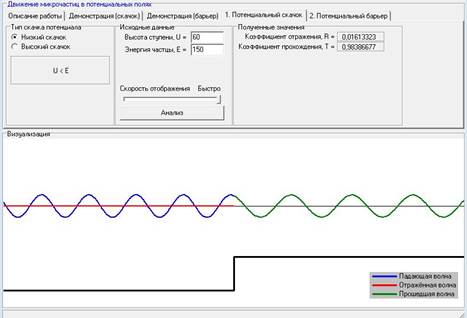
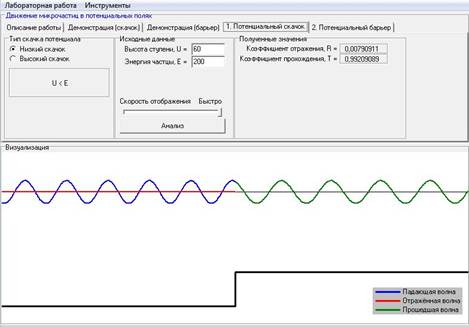
Для постоянной высоте ступени U с увеличением энергии частицы E коэффициент отражения R уменьшается, а коэффициент прохождения Т – увеличивается.

U >E

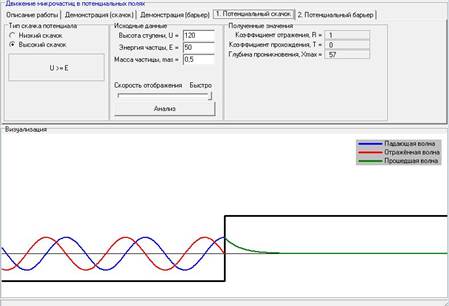
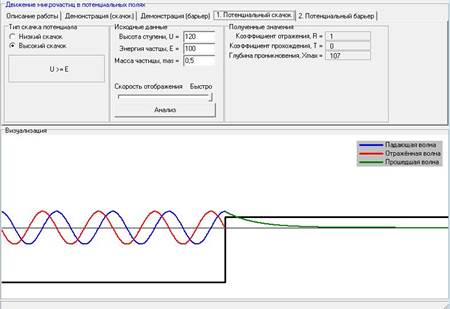
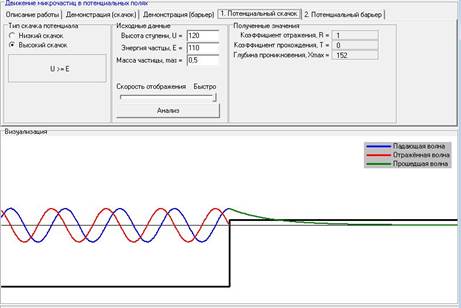
Для данного случая с неизменной высотой ступени U и изменчивым значением энергии E, коэффициент отражения остается неизменным (=1), коэффициент прохождения T=0.

Зависимость  глубины проникновения X в классически недоступную область от изменения энергии частицы (E) при постоянных высоте ступени (U) и массе частицы. Построить график зависимости X= f(E).

С неизменной высотой ступени U и изменчивым значением энергии E глубина проникновения увеличивается.

II).  Зависимость коэффициента  отражения  (R) от  варьирования  высоты  потенциала (U) при постоянных значениях энергии (E)  и массы частицы

E>U

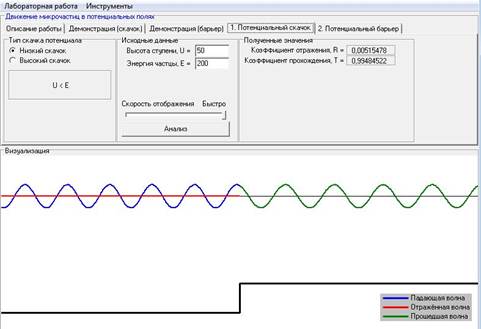
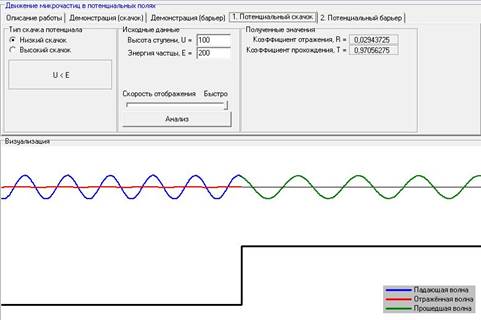
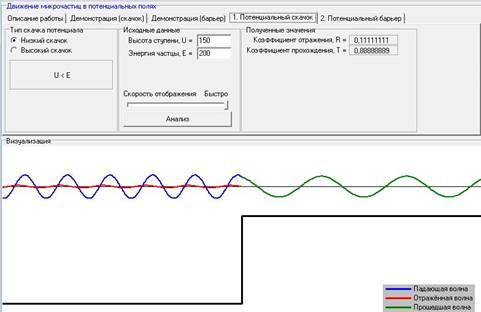
Для постоянного значения энергии частицы, с увеличением высоты ступени, коэффициент отражения увеличивается, а коэффициент прохождения уменьшается.

U >E

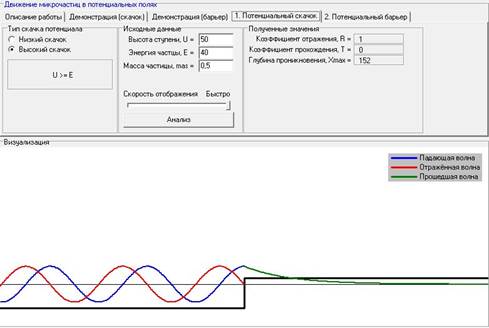
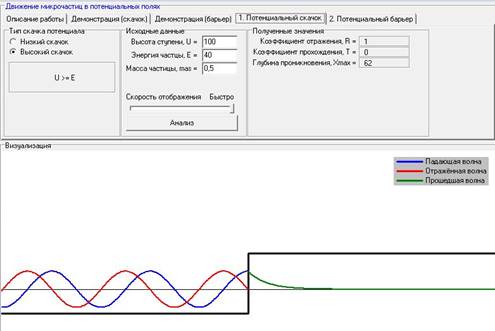
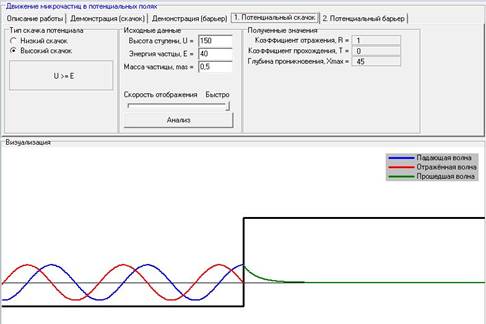
Для постоянного значения энергии частицы, с увеличением высоты степени ни коэффициент отражения, ни коэффициент прохождения не меняются.

Зависимость  глубины проникновения X от изменения высоты  ступени  (U) при постоянных значениях энергии частицы (E) и ее массы.

Для постоянного значения энергии частицы, с увеличением высоты ступени глубина проникновения уменьшается.

III). Зависимость глубины проникновения  X в классически недоступную область от изменения массы  частицы при постоянных значениях высоты ступени (U) и  энергии частицы (E).

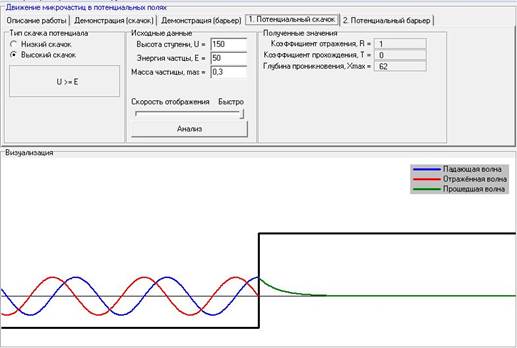
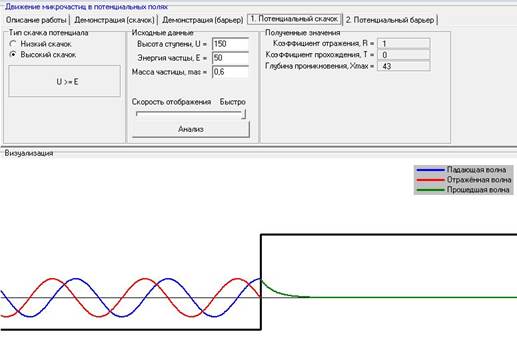
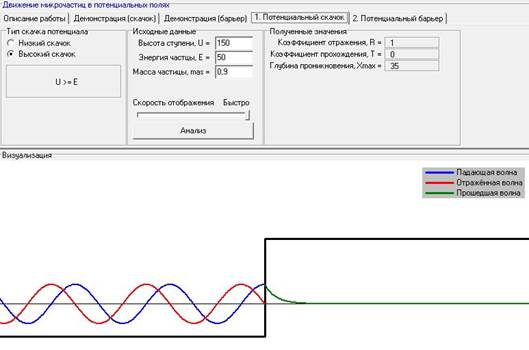
При постоянной энергии и высоте ступени с увеличением массы частицы идет уменьшение глубины проникновения.

IV). Зависимость величины коэффициента отражения (R) и коэффициента просачивания (D1) от барьера при варьировании  энергии  частицы (E) при постоянных: высоте барьера (U), ширине барьера-L, массе частицы. 

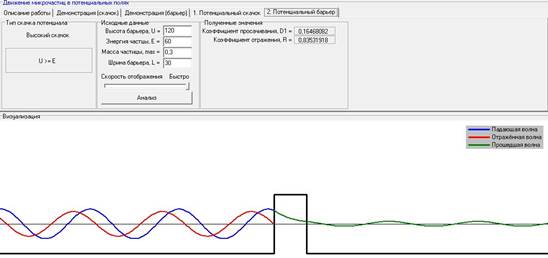
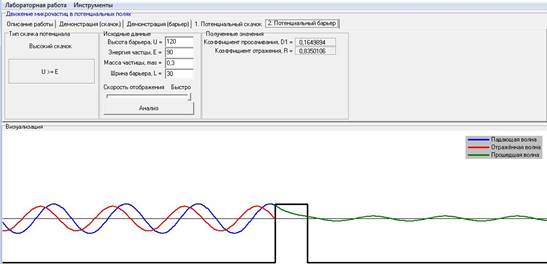
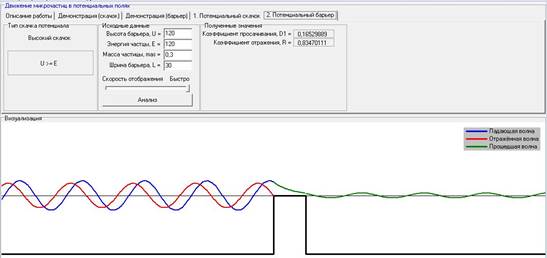
При варьировании  энергии  частицы (E) при постоянных: высоте барьера (U), ширине барьера-L, массе частицы, коэффициент прослаивания увеличивается, а коэффициент отражения уменьшается.

V). Зависимость величины коэффициента отражения (R) и коэффициента просачивания (D1) от барьера при варьировании высоты потенциального барьера (U) при постоянных:  энергии частицы (E), ширине барьера - L, массе частицы.

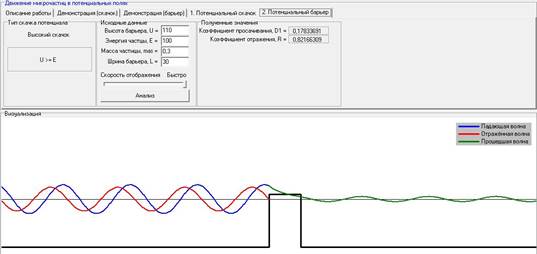
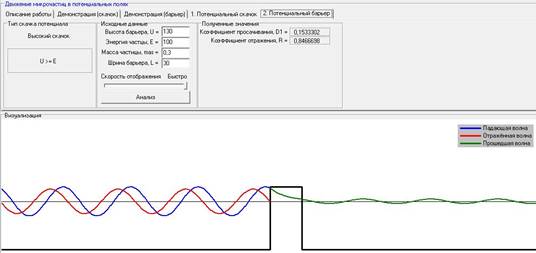
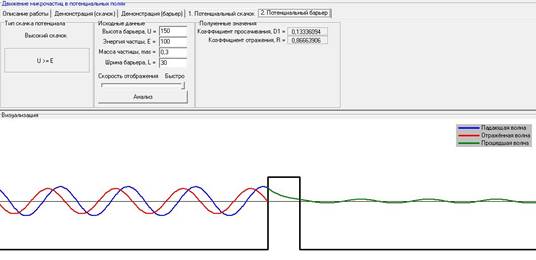
При варьировании высоты потенциального барьера (U) при постоянных:  энергии частицы (E), ширине барьера - L, массе частицы, коэффициент прослаивания уменьшается, а коэффициент отражения увеличивается.

VI). Зависимость величины коэффициента отражения (R) коэффициента просачивания (D1) от барьера  при  варьировании   ширины   барьера  L   при постоянных: высоте барьера (U), энергии частицы (E), массе частицы.

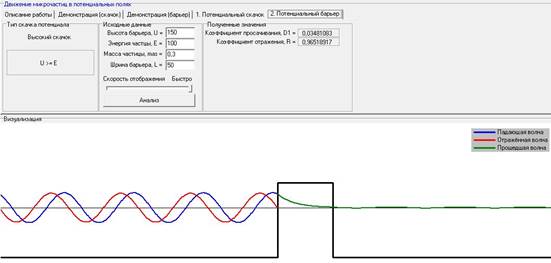
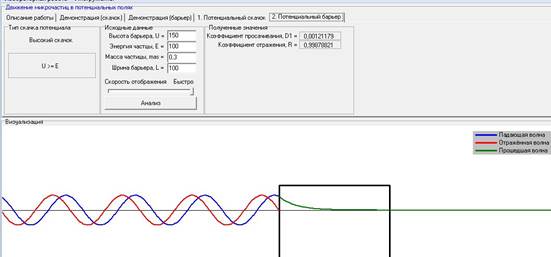
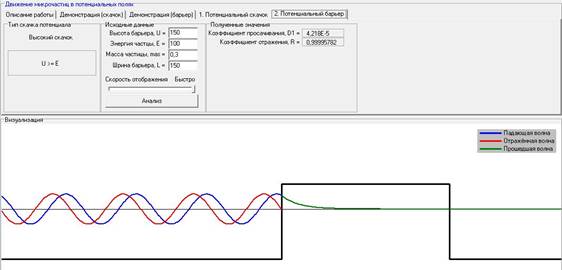
При  варьировании   ширины   барьера  L   при постоянных: высоте барьера (U), энергии частицы (E), массе частицы, коэффициент прослаивания уменьшается, а коэффициент отражения увеличивается.

VII). Зависимость величины коэффициента просачивания (D1) сквозь барьер при варьировании массы  частицы при постоянных: ширине барьера -L, высоте барьера (U), энергии частицы(E).

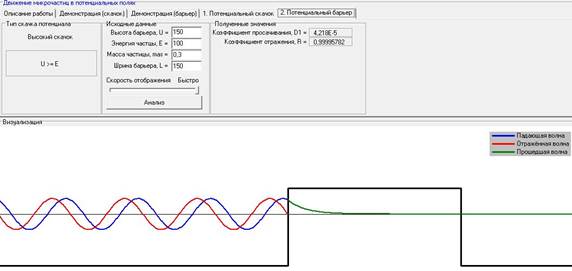
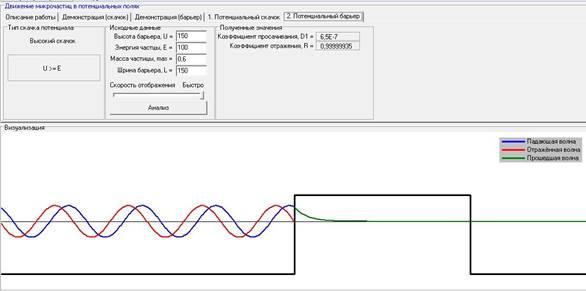
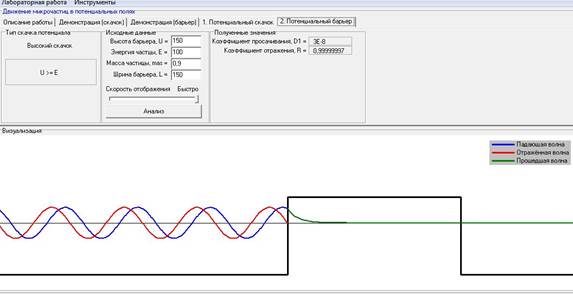
При варьировании массы  частицы при постоянных: ширине барьера -L, высоте барьера (U), энергии частицы(E), коэффициент просачивания увеличивается.

ВЫВОД: в ходе лабораторной работы были исследованы зависимости поведения микрочастицы при варьировании различных параметров (E,U,m,L) в случаях, когда E>U и E<U; построены графики зависимости и сделаны выводы после каждого анализа.