
Лекция 9
Вся информация об энергетическом спектре сводится в приведенную зону Бриллюэна. И мы с вами показали, что приведенная зона Бриллюэна на самом деле есть элементарная ячейка обратного пространства.
Зона Бриллюэна, в обратном пространстве
В пределах приведенной зоны Бриллюэна действует энергетический спектр, поэтому зона Бриллюэна вызывает огромный интерес. По кристаллу распространяются Блоховские волны, у которых главное это периодичность амплитуды. Амплитуда смоделирована периодом решетки. Вектор трансляции имеет те же самые размеры что и зоны Бриллюэна.
В трех мерном пространстве прямом пространстве заданы базисные вектора a,b,c, кроме того заданы базисные вектора элементарной ячейки обратного пространства a*,b*,c*, а вот теперь запишем что физический смысл зоны Бриллюэна есть ни что иное как элементарная ячейка обратного пространства. Соответственно в этом пространстве мы возьмем три направления Kx,Ky,Kz. Рассмотрим простейший случай, когда это будет кубическая сингония.

 Нарисуем вектора a*,b*,c*, и в произвольном случае они
могут быть разные. Построим элементарную ячейку на этих трансляциях. Получаем естественно,
какую либо фигуру. Итак, вот они Kx,Ky,Kz, я откладываю здесь вектора для кубической сингонии:
базисные вектора равны 2pi/a,
то есть размеру зоны Бриллюэна, и мы получаем элементарную ячейку. Принято и
обратную решетку строить подобным образом. Построение геометрически не сложное,
оно строится по одному правилу: вектора кончающиеся на Бреговких плоскостях
перпендикулярны этим плоскостям. То есть когда у нас волновой вектор, волна
электронная, падает на атомную плоскость, в результате отражения получаются
вторая, третья и так далее зоны. Элементарная ячейка обратного пространства
представляет собой зону Бриллюэна, строится по своим правилам и все что есть,
то и есть.
Нарисуем вектора a*,b*,c*, и в произвольном случае они
могут быть разные. Построим элементарную ячейку на этих трансляциях. Получаем естественно,
какую либо фигуру. Итак, вот они Kx,Ky,Kz, я откладываю здесь вектора для кубической сингонии:
базисные вектора равны 2pi/a,
то есть размеру зоны Бриллюэна, и мы получаем элементарную ячейку. Принято и
обратную решетку строить подобным образом. Построение геометрически не сложное,
оно строится по одному правилу: вектора кончающиеся на Бреговких плоскостях
перпендикулярны этим плоскостям. То есть когда у нас волновой вектор, волна
электронная, падает на атомную плоскость, в результате отражения получаются
вторая, третья и так далее зоны. Элементарная ячейка обратного пространства
представляет собой зону Бриллюэна, строится по своим правилам и все что есть,
то и есть.
Статистика электронов в кристалле
В этой теме мы будем говорить о Фермерских параметрах электрона, а для этого рассмотрим статистические распределения, которые описывают электроны. Из курса физики вы знаете, что статистическая физика – это физика большого количества частиц, или состояний. Так вот, статистические распределения, они своим результатом дают вероятность нахождения частиц в заданном состоянии. Электроны это те самые частицы, которые обладают полуцелым спином, то есть ±½. Выражение энергии Ферми:
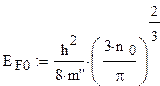
Получается, что для всех электронов, энергия которых меньше чем это значение энергии Ферми все состояния заполнены электронами, а для всех энергетических состояния, для которых энергия больше энергии Ферми, они свободны. Энергия ферми разделяет все занятые состояния от свободных. Вероятность заполнения уровня, лежащего рядом с энергией Ферми, но меньше энергии Ферми, больше половины и наоборот.
Описание электронов в кристалле
Принято считать, что если электроны описываются по формуле Ферми-Дирака, то они находятся в вырожденном состоянии. Вырожденные это когда отдельная квантовая частица потеряла свою индивидуальность. Все частицы находятся как бы в одном состоянии, особенно при температуре абсолютного нуля. Если энергия Ферми больше чем тепловое возбуждение, мы говорим о том, что электрон вырожден, если мы будем энергию равную и меньше, то это будет невырожденное состояние. Слабое вырождение, это когда эти две энергии соизмеримы. Значение энергии Ферми зависит от количества электронов, которые реально есть в этом свободном электронном газе. Функция Ферми говорит о возможности занятия ячеек, а заняты они или свободны, определяет функция плотности состояния.
Фермерские параметры электрона
Вырожденное или невырожденное состояние электронного газа будет определяться тем материалом, с которым вы работаете. Так вот в полупроводниках, как правило, невырожденный электронный газ, энергия Ферми там, как правило, очень небольшая, а в металлах энергия Ферми имеет большое значение, так как концентрация электронов там большая. Все начинается с энергии ферми, затем К Ферми, Т Ферми, импульс Ферми, скорость Ферми. И еще некий параметр, который называется «плотность состоянии в К пространстве (пространстве волнового вектора)». Плотность состояний будет определять нам некий объем деленный на минимальный фазовый объем, и мы узнаем, сколько состояний приходится на какое-то там пространство. Нанесем на этот график функцию G(E).
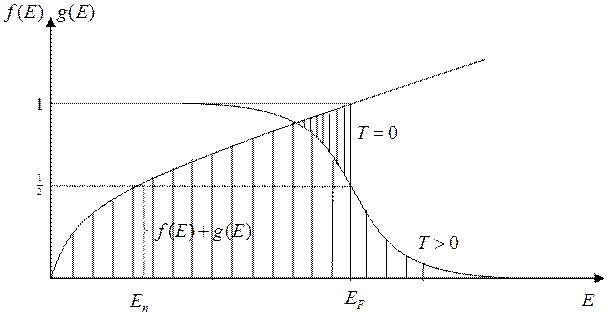
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.