Динамики кристаллической решетки (тепловые колебания решетки)

Лекция 12

Правило Мартисона , которое говорит что обратная результирующая времени релаксации рано сумме обратных времен всех видов механизмов.

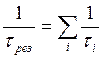
В случае, когда отдельный механизм преобладает γ очень мала по сравнению с другими. А если  они сравнимы, разные механизмы рассеивания имеют сравнимые времена релаксации, то работает на уровни φ. Рассмотрим пример что у нас есть разные механизмы рассеивания, допустим от температуры. Здесь время релаксации функция температуры. Чем больше температура, тем меньше время релаксации. Но допустим что материал не идеальный, и существую еще различного рода процессы рассеивания, связанные с рассеивание дефектов структуры. И какая-то определенная концентрация этих дефектов дает нам какое-то время релаксации.

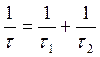Спрашивает как идет результирующая кривая. Она так и определяется, при температуре Т₁ преобладает механизм рассеивания у которого время релаксации наименьшее. Чем меньше время релаксации, тем быстрее проходит процесс потери направленного движения. Возьмем теперь температуру Т3 – вертикальная прямая. Анализируем две точки. Первая точка говорит о времени релаксации, связанном с рассеиванием на дефектах, а вторая точка соответствует времени релаксации при рассеивании тепловых колебаний. Что эффективнее рассеивает наш носитель? Ясно что дефект структуры и поэтому мы берем вот эту точку. И как пойдет результирующая? А результирующая пойдет точно также. Так же существует точка, где оба механизма абсолютно идентичны. Теперь рассмотрим каждый механизм рассеивания по отдельности.

Начнем с Динамики кристаллической решетки (тепловые колебания решетки). На примере шара рассмотрим такую особенность, что в сетке каждый из атомов может двигаться в любой плоскости. В шаре бесконечное множество плоскостей симметрии. И сложные колебания возникающие за счет этих самых движений вызывают движение волн по кристаллу. И вот для описания этого всего используется электронно-механический режим рассеивания. И для его применения следует рассмотреть два вида упрощения.

Первое упрощение использует, когда кристалл рассматривается как физическое тело.

Второе упрощение используется, когда имеется одномерное тело и все рассматривается относительно него.

Модель изолированного атома Рассматриваем сначала классическую модель. Вот кубическая решетка, и в центре на упругих связях, которые находятся в вершинах этого кубика подвешены атомы. В модели изолированного атома считается что все атомы идентичны, никаких привилегий ни у кого нет, и главная идея заключается в том, что вес атомы, окружающие центральный, считаются депозитами. Поговорим теперь особенно внимательно о гармоническом передвижении. Уравнение (1) это разложении функции U(t) в ряд Тейлора по малому параметру, малым параметром считается отклонение атомов от положения равновесия.

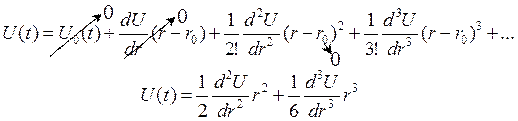Когда мы рассматриваем модель изолированного атома, мы в результате получаем связь между вращающей силой и расстоянием, или по другому это называется законов Гука. Далее рассматриваем случай при делении одного атома. В таком случае нам необходимо рассмотреть цепочку атомов. И в данном случае необходимо рассмотреть тему: «Волны в одномерной цепочке атомов». Рассматриваем цепочку атомов на расстоянии r, с периодом трансляции а и все обладают одинаковыми упругими связями b.