Вопросы к теоретическому зачету по дисциплине "Математический аппарат радиотехники", страница 2

23.  Какое пространство называется нормированным? Приведите не менее двух примеров нормированных пространств, указав в них способ введения нормы.

24.  Как определяется евклидово расстояние в  R_n, L₂?

25.  Дайте определение линейного пространства. Перечислите аксиомы ЛП.

26.  Приведите примеры линейных пространств (не менее двух).

27.  Дайте определение линейной комбинации векторов из L.

28.  Дайте определение линейной независимости системы векторов из L.

29.  Дайте определение базиса конечномерного ЛП. Какие важнейшие свойства базиса должны выполняться в ЛП?

30.  Приведите не менее трех примеров базисных систем для различных ЛП (с формулами или рисунками).

31.  Дайте определение скалярного произведения для ЛП. Перечислите свойства скалярного произведения.

32.  Приведите и докажите неравенство Коши-Буняковского для произвольных линейных пространств.

33.  Как в евклидовых пространствах норму и метрику согласовывают со скалярным произведением?

34.  Дайте определения пары ортогональных векторов, системы ортогональных векторов, ортонормальной системы. Докажите, что для ортогональной системы справедливо равенство .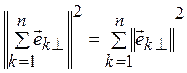

35.  Запишите представление вектора  через ортогональные базисные вектора . Докажите для конечномерных ЛП равенство Парсеваля ||||² =.

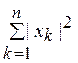36.  Докажите, что любая ортогональная система ненулевых векторов является линейно независимой.

37.  Докажите, что координаты вектора  относительно ортогонального базиса  равны х_п = 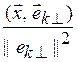, а для ортонормального  х_п = .

38.  Докажите, что скалярное произведение в R_n записывается как (, ) =, где х_k и y_k – координаты векторов  и  в ортонормальном базисе.

39.  Постройте первые четыре функции Хаара. Проверьте ортогональность любой пары из построенной системы функций.

40.  Проверьте линейную независимость векторов  = (0, –1, 3),  =  (1, 1, 0),  = (–1, –1, 1).

41.  Докажите ортогональность системы ,  на отрезке [–p, p]. Превратите ее в ортонормальную систему.

42.  Запишите неравенство Бесселя. Дайте определение замкнутой ортонормальной системы.

43.  Дайте определение оператора, функционала, функции. Как определяется понятие обратного оператора?

44.  Дайте определение линейного оператора.

45.  Приведите примеры линейных операторов.

46.  Как определяются сумма и произведение линейных операторов, степень оператора и функция от оператора?

47.  Дайте определение прямого и обратного оператора Фурье. Докажите линейность оператора Фурье.

48.  Дайте определение прямого и обратного оператора Гильберта. Докажите линейность оператора Гильберта.

49.  Дайте определение линейного функционала.

50.  Приведите примеры линейных функционалов.

51.  Сформулируйте обобщенное равенство Парсеваля и теорему Рэлея.

52.  Чему равны комплексный коэффициент передачи, амплитудно-частотная и фазочастотная характеристики линейного фильтра, осуществляющего преобразование Гильберта?

53.  Дайте определение аналитического сигнала. Как определить огибающую (модуль аналитического сигнала), характеризующую закон амплитудной модуляции и фазу (аргумент аналитического сигнала), определяющие закон угловой модуляции?

54.  Докажите, что функция s(t) и функция, преобразованная по Гильберту, ортогональны.

55.  Дайте определение дельта-функции. В чем заключается ее фильтрующее свойство? Определите спектральную плотность сигнала .

56.  Пусть сигнал s(t) имеет спектр . Найдите спектр смещенного сигнала s(t – t). Найдите спектр сигнала .

57.  Пусть сигнал s(t) имеет спектр . Найдите спектр сигнала . Найдите спектр сигнала s(t) cos w₀t.

58.  Пусть сигнал s(t) имеет спектр . Найдите спектр сигнала s(kt), где k > 0. Определите спектральную плотность прямоугольного видеоимпульса длительностью kt_и

59.  Пусть сигнал s(t) имеет спектр . Найдите спектр производной и интеграла этого сигнала.

60.  Найдите преобразование Фурье свертки и произведения функций f(t) и g(t).