

23 Анализ переходных процессов в развлетвленных цепях 1 порядка.
Если в цепи только 1 реактивный элемент L/C а остальные R и источники
– то цепь 1 порядка. Анализ такой цепи можно провести без получения в
явном виде диф. у-ра и все компоненты решения можно найти из цепи.
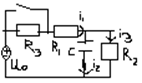
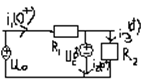
Опр i1(t) i2(t) i3(t)
1)Опр незав нач усл Uc(0-)
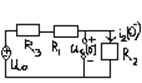 t<0 докомутационный установившийся режим
t<0 докомутационный установившийся режим
I2=C*dUc/dt=0 при Uc=const.
Uc(0-)=i3(0-)*R2=U0*R2/(R1+R2+R3)
2)Решение для t>0 i1(t)=i1вын+i1св
i1(t)=i1вын+A*e^(p*t) Опр i1вын
1вын=i1уст т.к. воздействие U0=const
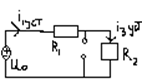
I1уст=i2уст=U0/(R1+R2)
I1(t)= U0/(R1+R2)+ A*e^(-t/тау)
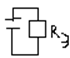 цепь в свободном режиме
цепь в свободном режиме
Rэкв=(R1*R2)/(R1+R2)
Тау=Rэкв*С тау=(R1*R2*C)/(R1+R2)
-p=(R1+R2)/(R1*R2*C)
Опр А? i1(0+)=Uo/(R1+R2)+A; t=0+
 Uc(0+)=Uc(0-)
Uc(0+)=Uc(0-)
I1(0+)*R1+Uc(0+)-Uo=0
I1(0+) =(Uo-Uc(0+))/R1 A=i1(0+)-Uo/(R1+R2)
R1*i1+R2*i2=Uo; i3=(Uo-R1*i1)/R2
I2=i1-i3.
24 Свободный процесс в последовательном RLC- контуре
(Случай колебательного режима) декремент затухания.
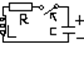 Uc(O-)!=0 полярность на рис
Uc(O-)!=0 полярность на рис
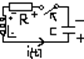
t>0 Опр i(t),Ur(t),U1(t),Uc(t)
Uc(0-)=-Uco
UR+UL+Uc=0; R*i+L*di/dt+1/cSidt=0
(S-интеграл)
d^2i/dt^2 + (R*di)/(L*dt) + i/(L*C)=0
Решение Ур-я 1)независ нач усл iL(0-)=0; Uc(0-)=-Uco
2)i(t)=iвын+iсв=iсв
Iсв=A1*e^(p1*t) +A2*e^(p2*t) (p1!=p2)
Хар-е ур-е: p^2+(R*p)/L+1/(L*C)=0
p1,2= -R/(2*L) ± ((R/(2*L))^2 -1/(L*C))^1/2
R/(2*L)=α 1/(L-C)^1/2=ω-резонансная частота
p1,2=-α ± (α^2- ω^2)^1/2
i(0+)=A1+A2 (1) di/dt=i`(t)=p1*A1*e^(p1*t)+p2*A2*e(p2*t)
i`(0+)=p1*A1+p2*A2 (2)
система: А1+A2=i(0+), p1A1+p2A2=i`(0)
Опр i(0+) и i`(0+); i(0+)=i(0-) т.к. это ток через L
Ri+L*di/dt+Uc(t)=0 di/dt=-R*i(t)/L-Uc(t)/L
i`(0+)=-R*i(0+)/L-Uc(0+)/L=Uco/L
система:A1+A2=0, p1A1+p2A2=Uco/L
(p1-p2)A1=Uco/L A1=Uco/(L*(p1-p2))
Процесс в цепи зависит от значений корней хар-кого Ур-я.
Колебательный режим
α < ω R<2*(L/C)^1/2
корни комплексные
p1=- α+( ω^2- α^2)^1/2=- α+j* ωd
p2=- α-( ω^2- α^2)^1/2=- α-j* ωd
A1=Uco/L*(p1-p2); A2=-A1=Uco/L(p1-p2)
A1=Uco/(L(-α+j* ωd+ α+j* ωd)= Uco/(L*2* j* ωd)
i(t)= Uco/(2* j* ωd*L)*e^(- α+j* ωd)- Uco/(2* j* ωd*L)*e^(- α-j* ωd)=
Uco/(2* j* ωd*L)*e^( -α*t) * (e^(j* ωd*t)- e^(-j* ωd*t))=
Uco/(ωd*L) * e^( -α*t) * sin (ωd*t)
τ= 1/α Td=2π/ωd
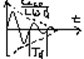 В RLC-контуре
сопровождается потерей энергии,
В RLC-контуре
сопровождается потерей энергии,
Что приводит к затуханию. При этом вводится понятие
Декремент затухания Δ.
Δ=i(t)/i(t+Td)=e^( α*Td) – не зависит от времени.
25 Свободный процесс в последовательном RLC- контуре
(Случай апериодитеского режима)
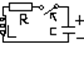 Uc(O-)!=0 полярность на рис
Uc(O-)!=0 полярность на рис
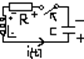
t>0 Опр i(t),Ur(t),U1(t),Uc(t)
Uc(0-)=-Uco
UR+UL+Uc=0; R*i+L*di/dt+1/cSidt=0
(S-интеграл)
d^2i/dt^2 + (R*di)/(L*dt) + i/(L*C)=0
Решение Ур-я 1)независ нач усл iL(0-)=0; Uc(0-)=-Uco
2)i(t)=iвын+iсв=iсв
Iсв=A1*e^(p1*t) +A2*e^(p2*t) (p1!=p2)
Хар-е ур-е: p^2+(R*p)/L+1/(L*C)=0
p1,2= -R/(2*L) ± ((R/(2*L))^2 -1/(L*C))^1/2
R/(2*L)=α 1/(L-C)^1/2=ω-резонансная частота
p1,2=-α ± (α^2- ω^2)^1/2
i(0+)=A1+A2 (1) di/dt=i`(t)=p1*A1*e^(p1*t)+p2*A2*e(p2*t)
i`(0+)=p1*A1+p2*A2 (2)
система: А1+A2=i(0+), p1A1+p2A2=i`(0)
Опр i(0+) и i`(0+); i(0+)=i(0-) т.к. это ток через L
Ri+L*di/dt+Uc(t)=0 di/dt=-R*i(t)/L-Uc(t)/L
i`(0+)=-R*i(0+)/L-Uc(0+)/L=Uco/L
система:A1+A2=0, p1A1+p2A2=Uco/L
(p1-p2)A1=Uco/L A1=Uco/(L*(p1-p2))
Процесс в цепи зависит от значений корней хар-кого Ур-я.
Апериодический режим
α > ω R>2*(L/C)^1/2
вещественные не равные корни
p1=- α+( ω^2- α^2)^1/2= -α+β =- α1
p2=- α-( ω^2- α^2)^1/2=- α- β =- α2
A1=Uco/(-α+β+α+β)= Uco/ 2Lβ; A2=- Uco/ 2Lβ
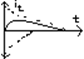
i(t)= Uco/ 2Lβ *e^(- α1*t) - Uco/ 2Lβ *e^(- α2*t)
| α2|>| α1| ; τ= 1/α1 τ2= 1/α2 τ1> τ2
26 Свободный процесс в последовательном RLC- контуре
(Случай критического режима) декремент затухания.
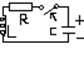 Uc(O-)!=0 полярность на рис
Uc(O-)!=0 полярность на рис
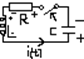
t>0 Опр i(t),Ur(t),U1(t),Uc(t)
Uc(0-)=-Uco
UR+UL+Uc=0; R*i+L*di/dt+1/cSidt=0
(S-интеграл)
d^2i/dt^2 + (R*di)/(L*dt) + i/(L*C)=0
Решение Ур-я 1)независ нач усл iL(0-)=0; Uc(0-)=-Uco
2)i(t)=iвын+iсв=iсв
Iсв=A1*e^(p1*t) +A2*e^(p2*t) (p1!=p2)
Хар-е ур-е: p^2+(R*p)/L+1/(L*C)=0
p1,2= -R/(2*L) ± ((R/(2*L))^2 -1/(L*C))^1/2
R/(2*L)=α 1/(L-C)^1/2=ω-резонансная частота
p1,2=-α ± (α^2- ω^2)^1/2
i(0+)=A1+A2 (1) di/dt=i`(t)=p1*A1*e^(p1*t)+p2*A2*e(p2*t)
i`(0+)=p1*A1+p2*A2 (2)
система: А1+A2=i(0+), p1A1+p2A2=i`(0)
Опр i(0+) и i`(0+); i(0+)=i(0-) т.к. это ток через L
Ri+L*di/dt+Uc(t)=0 di/dt=-R*i(t)/L-Uc(t)/L
i`(0+)=-R*i(0+)/L-Uc(0+)/L=Uco/L
система:A1+A2=0, p1A1+p2A2=Uco/L
(p1-p2)A1=Uco/L A1=Uco/(L*(p1-p2))
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.