Этапы формирования системы международного хозяйства. Теория сравнительных издержек (преимуществ). Выигрыш от международной торговли, страница 4

Рассмотрим еще один вырожденный случай, когда прямая лежит выше прямых сравнительных издержек обоих стран. В этих условиях международная торговля существовать не будет, т.к. страна 2 будет нести убытки (при предположении, что - точка обмена: в терминах У - СМ, или в терминах Х - АК; несмотря на то, что страна 1 могла бы при таких условиях торговли иметь выигрыш соответственно:

АЛЬТЕРНАТИВНОЕ ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ТСИ

или

ТЕОРИЯ АЛЬТЕРНАТИВНОЙ СТОИМОСТИ Haberler.

Она основывается на микроэкономике: граница производственных возможностей (productionpossibilitiestrontier) или кривая трансформации (transformationcurve).

Одни единицы измерения - это труд.

- граница производственных возможностей для страны 1.

- граница производственных возможностей для страны 2.

Тогда получаем:

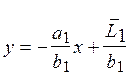 - уравнение прямой границы производственных возможностей для страны 1.

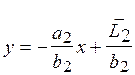 -уравнение прямой производственных возможностей для   страны 2.

Угол наклона(сравнительные издержки) - предельная норма трансформации  или альтернативная стоимость = от какого количества товара У нам необходимо отказаться для производства единицы товара Х.

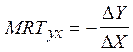 (предельная норма трансформации У на Х, т.е. для Х, т.к. “при увеличении Х”).

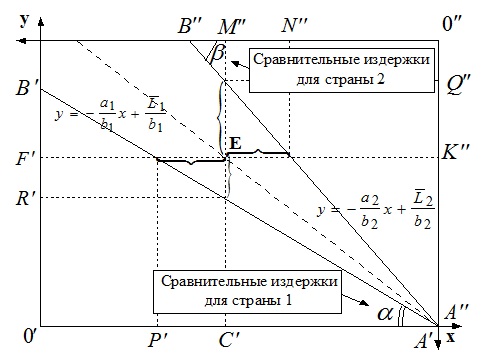
Повернем оси координат на . Видно, что , где  (ТТ должна находиться между прямыми сравнительных издержек двух стран)

Предположим, что торговля осуществляется в точке Е. У нас имеет место полная или частичная специализация, что в реальной жизни является не совсем верным предположением. Например, маленькая и большая страна.

- точка производства товара Х в стране 1.

- точка производства товара У в стране 2.

- то количество товара Х, которое  страна 1 съедает сама.

- то количество товара Х, которое страна 1 вносит на мировой рынок и обменивает на у страны 2.

- то количество товара У, которое страна 2 потребляет сама.

- количество товара У, которое страна 2 выносит на мировой рынок и меняет на

Е - точка потребления двух стран, которая выносится за границы производства обеих стран.

Представим выигрыш в этой интерпретации

1 страна	выигрыш в терминах товара Х:
	выигрыш в терминах товара У:
2 страна	выигрыш в терминах товара Х:
	выигрыш в терминах товара У:

Чем ближе кривая международной торговли к границе производственных возможностей, тем меньше выигрыш от участия в международной торговли у этой страны.

Модель Рикардо-Торренса развивается:

1.  Максимизация выигрыша от участия в международной торговли;

2.  Расширение, обобщение (m стран и n товаров);

3.  Попытка решения проблемы определения условий торговли, т.к. не был представлен спрос, а рассматривалось только предложение.

В рамках этой модели возможности анализа спроса минимальны, поэтому Джон Миль (Mill) в середине прошлого века предложил неоклассическую модель международной торговли.

НЕОКЛАССИЧЕСКАЯ ТЕОРИЯ (МОДЕЛЬ)

МЕЖДУНАРОДНОЙ ТОРГОВЛИ.

Для начала рассмотрим механизм установления общего равновесия в замкнутой экономике.

КРИВАЯ ТРАНСФОРМАЦИИ

(граница производственных возможностей)

И ДИАГРАММА ЭДЖВОРТА (Edgeisorth-Broisley).

Для анализа процессов, происходящих в производстве, его впервые применили…

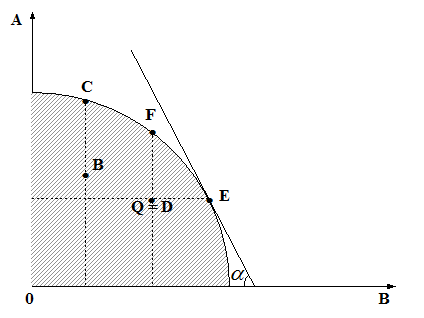
Кривая трансформации представляет собой максимальное количество одного товара, которое может быть получено при любом заданном количестве заданного другого товара.

.

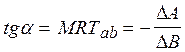Аналог для потребителя: 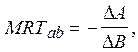 чтобы остаться на одной кривой безразличия.

Следовательно, оптимальное распределение ресурсов между отраслями, которые связаны с определенными условиями предельной полезности факторов.

Существует взаимно однозначное соответствие между кривой трансформации и картой изоквант.

Ящик  Эджворта:

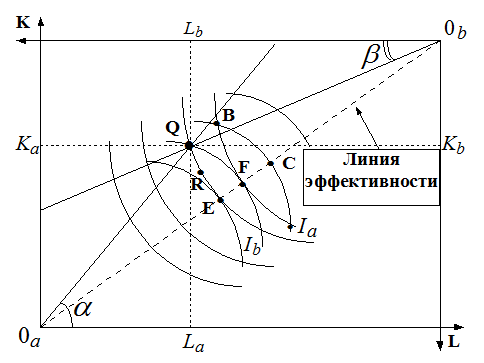
Боковые стороны соответствуют запасам данного вида ресурса в экономике.

I - изокванта = кривая безразличия для производителей = различные сочетания K и L для производства одного объема продукции.

Любая точка ящика Эджворта задает распределение ресурсов в экономике, рассмотрим. Например, точку Q:

- количество труда, которое идет на производство товара А.