Типовые МПФ. Наибольшее применение в теоретическом и прикладном макроэкономическом анализе имеют два вида МПФ: мультипликативная (чаще именуемая функцией Кобба-Дугласа) и функция с постоянной эластичностью заменяемости ресурсов (ПЭЗ). Эти функции обладают преимуществами с нескольких точек зрения: 1) они хорошо экономически интерпретируются; 2) имеют небольшое число параметров, что облегчает их статистическую оценку; 3) соответствующие им показатели экономического роста, эффективности, интенсификации имеют удобную аналитическую форму.
Общими свойствами функций Кобба — Дугласа и ПЭЗ являются однородность и постоянная эластичность заменяемости ресурсов (см. 4.3).
Динамическая функция Кобба - Дугласа
![]() (10.27)
(10.27)
отличается от ее статического
варианта (4.23) множителем A(t). Чаще всего принимается А(t) = ![]() ; с учетом этого
; с учетом этого
![]() (10.28)
(10.28)
Степень однородности функции Кобба — Дугласа определяется суммой аL + aK. Для статической модели обычно принимается аL + aK = 1. Но для динамической функции такое условие слишком жестко. Типично соотношение аL + aK>1, отражающее рост общей эффективности производственных факторов в динамике. Если сумма аL + aK ¹ 1, то можно осуществить нормировку коэффициентов эластичностей:
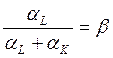 ,
, 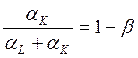
Тогда вместо (10-28) получаем
![]() . (10.29)
. (10.29)
Логарифмируя, а затем, дифференцируя по tфункцию (10.28), получаем соотношение между темпами прироста конечного продукта (национального дохода) и производственных факторов:
lny(t) =lna0+lt+aLlnL(t)+ +aKlnK(t),
![]() . (10.30)
. (10.30)
Таким
образом, темп прироста конечного продукта (национального дохода) есть сумма
автономного темпа и взвешенной суммы темпов прироста производственных факторов. Если ![]() и
и
![]() , то это означает
увеличение эффективности обоих производственных факторов (рост, как производительности труда, так и
фондоотдачи). Для экономики СССР в
течение продолжительного периода фондоотдача несколько снижается, вследствие чего
, то это означает
увеличение эффективности обоих производственных факторов (рост, как производительности труда, так и
фондоотдачи). Для экономики СССР в
течение продолжительного периода фондоотдача несколько снижается, вследствие чего ![]() .Из (10.28) следует, что при
.Из (10.28) следует, что при ![]() положительный темп X имеет место только
при aK<1. Если
же ак > 1, то l < 0.
положительный темп X имеет место только
при aK<1. Если
же ак > 1, то l < 0.
Функции (10.28), (10.29) имеют только один "динамический" параметр l. Учет динамики НТП, материализованного в производственных факторах, осуществляется в форме (10.25), (10.26). Дальнейшая динамизация МПФ может проводиться путем включения в нее переменных коэффициентов эластичности.
Динамическая функция с постоянной эластичностью заменяемости ресурсов имеет вид
![]() (10.31)
(10.31)
Она отличается от статического варианта (4.27) множителем А(t). Напомним, что aL, аK- параметры степени трудоемкости и фондоемкости макротехнологии; w — параметр, связанный с эластичностью замещения ресурсов; g— коэффициент "отдачи на масштаб" (степень однородности функции), характеризующий интенсификацию производства. Если s — эластичность замещения ресурсов, то
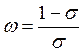 ,
, 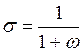
В простейшем случае
![]() , aK=1 – aL? g = 1.
, aK=1 – aL? g = 1.
Таким
образом, в функции ПЭЗ макротехнология характеризуется как минимум четырьмя
параметрами (![]() ). Нейтральный НТП измеряется параметрами
а0, l, g, ненейтральный —
параметрами аK, aL,w.
). Нейтральный НТП измеряется параметрами
а0, l, g, ненейтральный —
параметрами аK, aL,w.
Макроэкономическая функция ПЭЗ по сравнению с функцией Кобба — Дугласа обладает двумя преимуществами: 1) позволяет более явно разделить влияние НТП между двумя производственными факторами; 2) эластичность заменяемости ресурсов не задается априорно равной единице, а "оценивается".
Обобщение функции (10.31) возможно путем динамизации параметров аK, aL, w, g, в частности с помощью трендовых моделей. Более сложным является переход к функции с переменной эластичностью заменяемости ресурсов. Простейшим ее случаем является функция, в которой эластичность w является функцией времени.
Однофакторные макроэкономические функции. Наиболее простые МПФ выражают зависимости конечного продукта (национального дохода) от затрат живого труда и производственных фондов:
![]() ,
, ![]()
Построение и анализ таких функций могут предшествовать применению двухфакторных МПФ. Принципиальный недостаток данного подхода состоит в том, что динамика у(t) рассматривается в зависимости от динамики производственных факторов, взятых в отдельности.
Более
содержательным является выведение однофакторных функций показателей
эффективности производства из двухфакторных МПФ. С этой точки зрения наиболее удобна
функция Кобба - Дугласа первой степени. Из нее выводится функция производительности труда
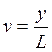 в зависимости от фондовооруженности
в зависимости от фондовооруженности 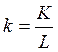 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.