Оценивание параметров модели Бокса-Дженкинса (общий метод)

ОЦЕНИВАНИЕ ПАРАМЕТРОВ МОДЕЛИ БОКСА-ДЖЕНКИНСА

(общий метод)

Здесь имеется три типа параметров:

ü  порядок разности d;

ü  авторегрессионные параметры φ, число которых равно p;

ü  параметры скользящего среднего θ, число которых равно q.

В общих чертах процедура выглядит следующим образом:

I.  Вначале вычисляются разности ряда до тех пор, пока они не окажутся стационарными относительно математического ожидания и дмсперсии, и отсюда получают оценку d.

II.  Задача тогда сводится к оцениванию параметров в модели авторегрессии – скользящего среднего:

,                                        (1)

где  - разность порядка d исходного ряда.

Оценить эти параметры по МНК невозможно из-за отсутствия последовательности значений .

Поэтому предлагается такая последовательность действий.

II.1 Величины ε, стоящие в правой части уравнения:

              (2)

будут отсутствовать в выражении . Если умножим обе части (2) на  и взять математические ожидания, то правая часть будет равна нулю.

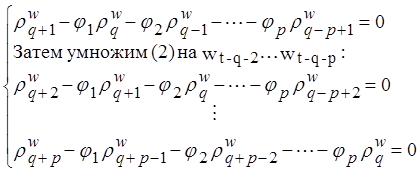
Получим систему, состоящую из p уравнений относительно p неизвестных параметров φ.

Указанием на смешанный процесс является тот факт, что автокорреляционная функция затухает.

Другой факт, помогающий идентифицировать смешанный процесс заключается в том, что после q задержек теоретические автокорреляции удовлетворяют разностному уравнению для чисто авторегрессионного процесса.

частный

случай

АРПСС

(1, d, 1)
Например, если предположим, что процесс имеет порядок (1, d, 1), т.е. , то подстановкой выборочных оценок  и  вместо  и   в выражения

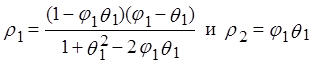
можно получить приближенные значения параметров процесса .

Решение этих уравнений, в которых в качестве  берутся эмпирические значения  автокорреляций для ряда значений , дает нам первые оценки параметров авторегрессии : .

II.2 С помощью этих оценок можно определить левую часть Уравнения (1) и получить временной ряд:

и для этого ряда рассчитывают первые (q+1) автокорреляций

II.3 Полученные на втором этапе автокорреляции  используются при альтернативном расчете начальных оценок параметров скользящего среднего .

Действительно, приняв , для которого, как мы знаем, первые q автокорреляций могут быть выражены через параметры модели:

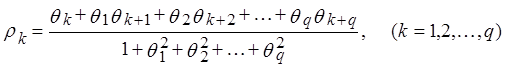
Решая полученную таким образом систему q уравнений относительно q неизвестных параметров θ, получаем их начальные оценки .

II.4 С помощью  находим последовательность значений

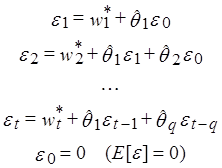
II.5 Наконец, получив с помощью предварительных оценок  и  последовательность значений , и имея в наличии ряд , методом наименьших квадратов находим эффективные оценки параметров модели (2).