Основные черты декомпозиционного подхода, страница 3

Основной вывод состоит в том, что теоретически возможно построить такие локальные критерии, которые содержат необходимую и достаточную информацию для того, чтобы каждая подсистема, максимизируя этот критерий и учитывая только собственные ограничения, могла бы получить план , являющийся частью народнохозяйственного оптимального плана. Это означает, что оптимальный народнохозяйственный план можно построить, указывая подсистемам только показатели типа цен, а в остальном предоставляя им полную свободу в выборе плановых решений. Однако из математического анализа данного вопроса следует, что такая возможность осуществима, когда модели подсистемы (15.8) являются только такими задачами выпуклого программирования, в которых либо множества допустимых планов подсистем строго выпуклы, либо целевые функции подсистем строго вогнуты. Уже для случая линейных задач такая возможность неосуществима, т.е. централизованное установление только показателей типа цен (c_k) недостаточно для согласования локальных оптимумов с глобальным; требуется более сильное вмешательство "центра" в процесс построения локаль­ных планов (см. [2. Гл. IV]).

Примеры декомпозиционного подхода в экономическом анализе.

Пример 1. При анализе общей модели оптимального планирования В.В.Новожилов ввел понятие дифференциальных затрат, включающих наряду с прямыми затратами по определенному направлению также затраты обратной связи, учитывающие дополнительные затраты в народном хозяйстве в связи с отвлечением ряда дефицитных народнохозяйственных ресурсов по оцениваемому направлению[1].

Рассмотрим задачу распределения ограниченных капиталовложений между заданными направлениями их использования i — 1, ..., т (например, объектами строительства). По каждому направлению существует зависимость уровня текущих затрат от величины выделяемых вложений . Обычно предполагается, что < 0, > 0. Задача состоит в распределении капиталовложений между направлениями их использования, обеспечивающими минимум суммарных текущих затрат

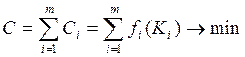           (15.11)

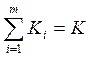
Легко видеть, что оптимальное распределение К* = () может быть получено как композиция изолированных локально-оптимальных решений , осуществляемых на основе локальных критериев

                 (15.12)

где величина норматива Е_н задается оптимальной оценкой l* ограничения по капитальным вложениям в задаче (15.12) (Е_н = — l*) и характеризует предельную экономию суммарных текущих затрат при использовании капиталовложений.

Если исходная задача (15.11) охватывает все направления капиталовложений и К означает общую величину капиталовложений по народному хозяйству, то Е_н интерпретируется как народнохозяйственный норматив эффективности капиталовложений, а локальные критерии (15.12) — как приведенные затраты на создание и функционирование объектов капиталовложений. Задание норматива эффективности Е_н на оптимальном уровне —l* и использование показателя приведенных затрат позволяют децентрализовать процесс составления оптимального плана распределения капиталовложений и обеспечить совместимость локальных и народнохозяйственных оптимумов.

Пример 2. Анализируя задачу оптимального распределения посевных площадей между различными культурами, Л.В.Канторович показал возможность применения рентных оценок для нахождения оптимального решения[2].

Для случая монокультурного хозяйства такие оценки должны удовлетворять условию

® max,        (15.13)

где  — зависимость затрат на i-м участке от объема производства Q_i(предполагается возрастающей с падающей эффективностью затрат) ; w — норматив предельных затрат на заданный объем сельскохозяйственной продукции по всем земельным участкам.

Оптимизационная задача, порождающая локальные критерии (15.13), имеет вид

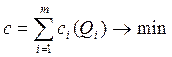    (15.14)

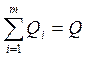
Норматив w* задается оптимальной оценкой 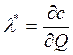 ограничения по производству сельскохозяйственной продукции.

Линейный аналог задачи (15.14) еще яснее выявляет смысл локального критерия (15.13) как рентной оценки земельного участка.

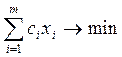
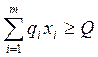    (15.15)

 i= 1, … m

Здесь x_i, S_i — размеры, используемые и возможные для использования участков земель i-го качества; c_i , q_i — затраты и урожайность в расчете на 1 га.

Пусть земельные участки занумерованы в порядке возрастания удельных затрат . В оптимальном плане задачи (15.15) в обработку включаются участки, первые в ряду восходящих удельных затрат

,

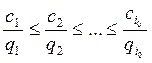причем все участки, кроме "замыкающего", используются полностью, а посевные площади замыкающего участка (с номером i₀) выбираются лишь в размере, обеспечивающем сбор урожая с него в объеме, дополняющим объемы производства на предшествующих участках до потребности (Q). Индивидуальные затраты худшего участка определяют норматив замыкающих затр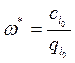ат , а рентные оценки используемых в оптимальном плане участков задаются разницей замыкающих и индивидуальных затрат 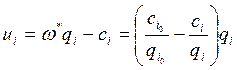,  i = 1, …, i₀.