Основные черты декомпозиционного подхода, страница 2

Условия согласования народнохозяйственного и локального оптимумов. В общем случае проблема согласования решений в системе моделей понимается как проблема согласования локальных оптимумов, получаемых при решении отдельных задач подсистем, и глобального народнохозяйственного оптимума. Тип моделей подсистем определяет процедуру согласования их решений, и, наоборот, выбранная схема согласования локальных решений влияет на структуру моделей подсистем, получаемых декомпозицией исходной модели.

При использовании лимитных методов декомпозиции для каждой подсистемы строится задача вида

f_k (x_k) ® max;

g_k (x_k) £ q_k           (15.6)

Здесь  — множество допустимых планов k-й подсистемы, определенных внутренними условиями развития подсистемы (не зависящих от параметров внешних связей); условия  описывают в явном виде зависимость планов подсистем от внешних условий. Очевидно, что .

В схемах вертикальной координации (с использованием задачи "центра") согласование решений локальных задач (15.6) осуществляется путем корректировки параметров q_k. Целью процесса координации является определение таких значений , которые позволяли бы получить оптимальные планы подсистем, допустимые по общесистемным условиям и максимизирующие целевую функцию f(X).

Народнохозяйственная модель, декомпозицией которой получены модели подсистем (15.6), имеет следующий вид:

;

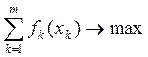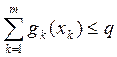                        (15.7)

Легко видеть, что модель (15.7) является частным случаем метамодели (15.2) в предположении сепарабельности функций f(x).

Пусть - решение локальной задачи (15.6) для k-й подсистемы и двойственной к ней;  - решение народнохозяйственной задачи (15.7), v* — вектор оптимальных оценок общесистемных ограничений.

Основные утверждения о соотношении решений задач (15.6) и (15.7) состоят в следующем.

1.  Если в локальных задачах (15.6) определить вектор внешних связей  то композиция их локально-оптимальных планов является одним из оптимальных решений метамодели (15.7).

2. Предположим, что решения локальных задач (15.6) с параметрами внешних связей такие, что 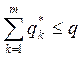удовлетворяют двум условиям:

а) при всех k= 1, ..., т векторы оптимальных оценок совпадают, т.е. , где и — число общесистемных ограничений задачи (3.7) ;

б) при выполнении условия (а), если какая-либо оценка , то и .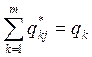

Тогда композиция локально-оптимальных планов  составляет оптимальный план метамодели (15.7).

Доказательство утверждений достаточно простое и основывается на сопоставлении свойств функций Лагранжа локальных и глобальных задач (см., например, [2. С. 167— 180]).

При использовании ценностных методов декомпозиции задача для каждой подсистемы принимает вид

f_k (x_k, c_k) ® max;

          (15.8)

Она включает только локальные ограничения, а критерий оптимальности выводится определенным способом из глобального критерия. Функция f_k (x_k, c_k) аккумулирует информацию об общесистемных ограничениях (в частности, учитывает затраты общих ресурсов). Локальным критерием производственных систем может быть максимизация прибыли или другого показателя хозяйственной деятельности подсистемы в денежном выражении (разности между суммарным хозяйственным результатом и суммарными затратами). Вектор c_kсодержит ценностные показатели, устанавливаемые "центром".

При использовании народнохозяйственной модели типа (15.7) локальный критерий f_k (x_k, c_k) в модели k-я подсистемы, обеспечивающей согласование локальных и глобального оптимумов, имеет вид

f_k{x_k, c_k) = f_k(x_k)-c_kg_k(x_k).(15.9)

Действительно, при выполнении условий теоремы Куна — Таккера можно построить задачу "почти безусловного" экстремума

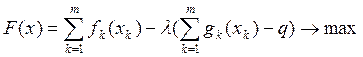           (15.10)

, k = 1, …, m

которая распадается на ряд подзадач

Если в локальной задаче подсистемы (15.8) с критерием (15.9) определить параметры c_kравными оптимальному значению вектора оценок задачи (15.10), то, во-первых, k-я компонента оптимального народнохозяйственного плана  является оптимальным решением локальной задачи; во-вторых, композиция локально-оптимальных планов составляет оптимальный план метамодели (15.7).