Основные понятия экономических взаимодействий

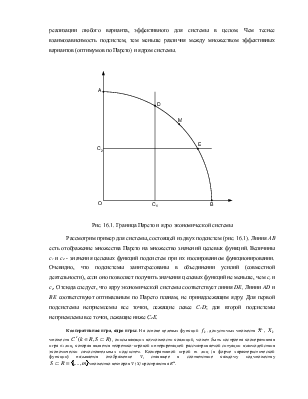
16.2. Основные понятия экономических взаимодействий

Экономический оптимум по Парето. Пусть в народном хозяйстве выделяется т подсистем. Введем следующие обозначения:

X_k – план k-й подсистемы;

c_k = f_k(X_k) – целевая функция k- й подсистемы;

 – план системы как композиция планов подсистем;

– вектор значений целевых функций подсистем;

– множество допустимых планов k-й подсистемы;

 – множество допустимых планов системы в целом, состоящих из композиции допустимых планов подсистем и удовлетворяющих дополнительным общесистемным ограничениям.

Из совокупности моделей подсистем можно составить задачу векторной оптимизации на множестве допустимых вариантов развития подсистем и системы в целом с целевой функцией

Решение этой задачи позволяет находить эффективные варианты (оптимальные по Парето).

Допустимое решение (ему соответствует вектор ) является эффективным, если не существует другого допустимого решения , которому отвечает вектор , такой, что для всех k=1,…,mи 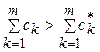[1].

Эффективное решение X^*совокупности подсистем – это такое допустимое решение всей системы, при котором ни одна из подсистем не может улучшить свое положение (увеличить значение своей локальной целевой функции), не ухудшая положения хотя бы одной из остальных подсистем. Можно сказать, что понятие оптимальности по Парето выражает такой принцип коллективной рациональности (такое экономическое поведение), согласно которому "хорошо делать так, чтобы кому-нибудь стало лучше, если при этом никому другому не становится хуже".

Ядро экономической системы. Принадлежность к множеству эффективных решений является разумным требованием к выбору согласованного планового решения в системе из нескольких экономически самостоятельных участников. В стремлении получить решение, оптимальное по Парето, выражается единство интересов различных подсистем. Но разные оптимальные по Парето решения неодинаково выгодны для разных подсистем. Поэтому введенное понятие оптимальности является довольно слабым, оно не исключает того, что какая-либо подсистема (или группа подсистем, коалиция), действуя самостоятельно, не сможет (не смогут) достигнуть более предпочтительных для них вариантов развития.

В подобных ситуациях какая-либо подсистема или группа подсистем может быть заинтересована и имеет возможности воспрепятствовать реализации некоторых оптимальных по Парето планов. Это означает, что требование оптимальности по Парето не учитывает возможности участников и коалиций влиять на выбор совместных планов подсистем. Эти возможности и их влияние на потенциальные исходы процессов согласования решений изучаются в рамках кооперативной теории игр многих лиц.

Формализованное описание возможностей коалиции  мо­жет быть осуществлено путем спецификации множества  векторов, составленных из значений целевых функций. При этом  в том и только в том случае, если существует допустимый план , , который данная коалиция может обеспечить "собственными" силами и такой, что  для всех .

Очевидно, что при свободном выборе решений вектор  не будет реализован, если существует коалиция Sи вектор  такие, что  и 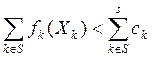. В этом случае говорят, что коалиция Sблокирует вектор X.

Введенные понятия возможностей коалиций и блокирования позволяют сформулировать второе требование к выбору согласованного решения