



продукции сверх
минимально необходимых объемов ![]() ), превращающие
неравенства в равенства.
), превращающие
неравенства в равенства.
В каждом i-м уравнении
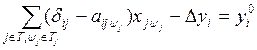
положительными являются только коэффициенты при переменных ![]() . Но поскольку все
. Но поскольку все ![]() ,
то и все
,
то и все
![]() ,
, ![]() ,
,
т.е. в оптимальном плане должны производиться все виды продуктов.
Максимальное число положительных переменных в оптимальном плане равно n (числу уравнений).
Следовательно, в каждой сумме переменных ![]() положительной может быть только
одна переменная. Иначе говоря, в оптимальном плане каждый продукт
производится только одним способом.
положительной может быть только
одна переменная. Иначе говоря, в оптимальном плане каждый продукт
производится только одним способом.
Следствие. Из
теоремы следует, что поскольку число возможных положительных переменных
исчерпывается переменными способов производства, то все ![]() (в оптимальном плане равны нулю. Иными
словами, оптимальный план обращает исходные неравенства в равенства.
(в оптимальном плане равны нулю. Иными
словами, оптимальный план обращает исходные неравенства в равенства.
Пусть X* — оптимальный план модели (каждая его
компонента есть интенсивность применения какого-то "лучшего" способа
производства); А* — матрица коэффициентов материальных затрат, составленная
из способов, которые вошли в оптимальный план. Матрица А* аналогична
матрице А межотраслевого баланса с той лишь разницей, что вместо
средневзвешенных коэффициентов из разных способов в ней представлены
коэффициенты только "лучших" способов. Матрицы А* и (Е -
А*) обладают теми же экономико-математическими свойствами, что и матрицы
межотраслевого баланса. Отметим, в частности, существование матрицы (Е - А*)-1
![]() 0. Элементы матрицы (Е -A*)-1
являются коэффициентами полных потребностей в выпуске продукции для
получения единицы конечной продукции в оптимальном плане. Оптимальный план
удовлетворяет следующей системе уравнений:
0. Элементы матрицы (Е -A*)-1
являются коэффициентами полных потребностей в выпуске продукции для
получения единицы конечной продукции в оптимальном плане. Оптимальный план
удовлетворяет следующей системе уравнений:
![]() или
или ![]() .
.
Теорема 2. Базис оптимального плана, а,следовательно, и выбор "лучших" способов остаются постоянными при любых изменениях положительного вектора Y0.
Доказательство. Для того чтобы базис оптимального плана оставался неизменным при переменном векторе Y0, достаточно в
соответствии с (8.9), чтобы выполнялось условие (Е - A*)-lY0 ![]() 0. Поскольку матрица (Е - А*)-1
0. Поскольку матрица (Е - А*)-1
![]() 0, условие (Е - A *)-lY0
0, условие (Е - A *)-lY0![]() 0 выполняется всегда при любом Y0
0 выполняется всегда при любом Y0![]() 0 и тем более при Y0 > 0.
0 и тем более при Y0 > 0.
Пусть для
некоторого Y0 > 0 получено решение X*. Базис
полученного решения (Е - А*) остается неизменным и тогда, когда
вектор будет изменяться любым образом
в положительной области (0 < Y0 < + ¥). Если базис
оптимального плана — неразложимая матрица, то теорема распространяется на случай Y0![]() 0. Это означает, что, вычислив матрицу (Е - А
*)-1 для одного варианта конечной продукции, можно
неоднократно использовать ее для расчета производственной программы при других вариантах конечной
продукции.
0. Это означает, что, вычислив матрицу (Е - А
*)-1 для одного варианта конечной продукции, можно
неоднократно использовать ее для расчета производственной программы при других вариантах конечной
продукции.
Из задачи, двойственной (8.29), следует, что для способов, вошедших в
оптимальный план (![]() ), выполняются условия
), выполняются условия
![]()
Поэтому вектор оптимальных оценок продукции V* = (![]() ) определяется решением системы уравнений V* = V*A * + t* или V* = t (E — А*)-1.
) определяется решением системы уравнений V* = V*A * + t* или V* = t (E — А*)-1.
Видим, что оптимальные оценки продукции в рассматриваемой модели равны коэффициентам полных трудовых затрат, исчисленным по лучшим производственным способам для каждого вида продукции.
Следствие. Оптимальные оценки vизменяются при любых изменениях положительного вектора Y0. Поскольку в соответствии с теоремой 2 базис оптимального плана остается постоянным при любых изменениях вектора Y0в положительной области, то, следовательно, не изменяются и оптимальные оценки (задача исчисления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.