Модели, использующие случайные импульсы. Начальные оценки параметров. Оценивание параметров процесса скользящего среднего

Предварительные оценки  можно получить, подставив в (9) вместо  и решив получающиеся нелинейные уравнения. Предварительную оценку можно тогда получить из , заменив  их предварительными оценками и его оценкой .

II.  НАЧАЛЬНЫЕ ОЦЕНКИ ДЛЯ ПРОЦЕССОВ АВТОРЕГРЕССИИ

Если предположить, что исследуемый ряд – процесс авторегрессии второго или первого порядка, начальные оценки иможно получить, заменив теоретические автокорреляции  их выборочными оценками , полученными из уравнений Юла-Уокера.

В частности, для процесса АР(1):

И для АР(2): 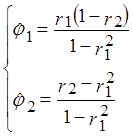                                                         (10)

Соответствующая формула, вытекающая из уравнений Юла-Уокера, для процессов высшего порядка может быть получена заменой  на  отсюда:

,

где - выборочная корреляционная матрица размером , содержащая коэффициенты до порядка (p-1), и - вектор ().

Например, если p=3, то

Действительно, автокорреляционная функция

Если подставить в это уравнение значения k=1,2, …,p, то получим систему линейных уравнений для  со свободными членами , или так называемые уравнения Юла-Уокера

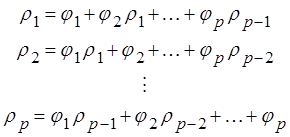
Оценки Юла-Уокера для параметров процесса получим, заменив теоретические значения автокорреляции выборочными автокорреляциями .

Если мы перейдем к матричным обозначениям

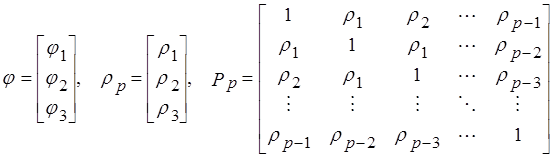
решение системы уравнений Юла-Уокера – выражения для параметров  через автокорреляции – можно записать в виде                                    (**)

Показано, что в отличии от ситуации возникающей с процессами СС, параметры авторегрессии, получаемые из (**), весьма близки к эффективным оценкам максимального правдоподобия.

III.  НАЧАЛЬНЫЕ ОЦЕНКИ ДЛЯ СМЕШАННЫХ ПРОЦЕССОВ АВТОРЕГРЕСИИ – СКОЛЬЗЯЩЕГО СРЕДНЕГО

В дальнейшем часто будет обнаруживаться, что-либо после взятия нужного числа разностей ряд   будет наиболее экономично описываться смешанным процессом АРСС

Указанием на смешанный процесс является тот факт, что автокорреляционная функция затухает. Другой факт, помогающий идентифицировать смешанный процесс, заключается в том, что после q задержек теоретические автокорреляции удовлетворяют разностному уравнению для чисто авторегрессионого процесса .

В частности, если автокорреляционная функция d-й разности спадает экспоненциально (если не считать искажения в ), следует предположить, что процесс имеет порядок (1, d, 1), т.е.

,                                    (***)

где .

Приближенные значения параметров процесса (***), полученные подстановкой выборочных оценок  и вместо  и в выражении

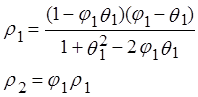
ОЦЕНИВАНИЕ МОДЕЛИ

После того, как процесс идентификации привел к пробному варианту модели, нам необходимо получить эффективные оценки параметров. После этого подогнанная модель будет подвергнута диагностической проверке и тестам на качество подгонки.

МОДЕЛЬ БОКСА-ДЖЕНКИНСА

Одной из основных проблем применения такой модели является определение эффективных оценок ее параметров.

Здесь имеется 3 типа параметров: порядок разности d, авторегрессионые параметры , число которых равно q.

В общих чертах процедура выглядит следующим образом:

1)  Вначале вычисляются разности ряда до тех пор, пока они не окажутся стационарными относительно математического ожидания и дисперсии, и отсюда получают оценку d.

Задача тогда сводится к оцениванию констант в модели авторегрессии – скользящего среднего:

                                              (*)

где  - разность порядка d исходного ряда.

Величины , стоящие в правой части (*), будут отсутствовать в выражении . Если умножить обе части (*) на и взять математическое ожидание, то правая часть будет равна нулю.

Обозначая автокорреляцию порядка k через , имеем

                    (**)

и (p-1) последующих уравнений, получаемых путем умножения  на и т.д. Решение этих уравнений дает нам первые оценки параметров авторегрессии (к сожалению, из-за выборочных колебаний эмпирических ковариаций более высокого порядка эти оценки не очень надежны).

2)  В таком случае с помощью этих оценок можно определить левую часть