Определение выражения установившегося напряжения резистора в схеме RC-цепи первого порядка, страница 2

В.

Свернём выражение принуждённой составляющей напряжения резистора при 0 £ t¢ £ T/2:

 В.

Следовательно,

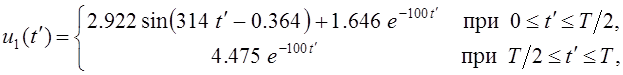 В.

Зависимость u₁(t¢) на интервале 0 £ t £ 20 мс с шагом 2 мс представлена таблицей; Рис. 6.4 отображает её на интервале 0 £ t¢ £ 20 мс.

Таблица

t¢, мс	0	2	4	6	8	10	12	14	16	18	20
u1(t¢), В	0.606	2.111	3.379	3.822	3.186	1.646	1.348	1.104	0.903	0.740	0.606

Проверка:

.606 В.

Численное решение этой задачи осуществляется также в указанные два этапа.

Обратимся сначала к полученному ранее уравнению для переменной состояния цепи в виде

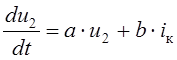
в котором

a = – 100 с^-1, b = 60×10³ Ом/с.

при неизвестном пока стартовом значении u₂(0+).

Численное решение уравнения для переменной состояния цепи при 0 £ t¢ £ T  найдём  с помощью функции rkfixed математического пакета MathCad 7 Pro, реализующей  метод  Рунге-Кутта  с  фиксированным шагом. Для определения  стартового  значения  переменной состояния u₂(0+) применим следующий итерационныё алгоритм. Положим сначала u₂(0+) = 0 и с помощью функции rkfixed найдём его финишное значение u₂(T–). Если оно не равно нулю,  что практически наиболее вероятно, то за новое стартовое значение примем полусумму предыдущих стартового и финишного значений. Далее поступаем аналогично. Процесс половинного деления отрезка [u₂(0+), u₂(T–)] продолжаем до тех пор, пока финишное и стартовое значения не совпадут с заданной точностью. Этот алгоритм воплощён в программе Е.Шафороста, студента группы ФЛ – 91 ФТФ НГТУ:

                         – допускаемая погрешность различия финишного и стартового значений переменной состояния цепи;

                        – значение периода изменения задающего тока;

                              – число точек (не считая начальной) деления отрезка [u₂(0+), u₂(T–)];

                               – первое приближение стартового значения переменной состояния u₂(0+);

 – выражение её первой производной;

                                 – последнее приближение стартового значения переменной состояния цепи u₂(0+);

Далее последовательно задаём:

                                 – стартовое значение переменной состояния цепи u₂(0+);

           –  выражение её первой производной;

   – вычисление значений переменной состояния цепи в двухстах точках (200) интервала времени [0,0.02];

                       – номера точек разбиения интервала времени пробегают значения от 0 до числа строк без 1 матрицы Z.

                                        – элементам вектора t присваивают значения элементов первого столбца матрицы Z.

                                      – элементам вектора u₂ присваивают значения элементов второго столбца матрицы Z.

Выражение искомой зависимой переменной u₁(t¢) есть линейная функция переменной состояния u₂(t¢) и задающего тока i_к(t¢):

,

где 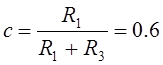   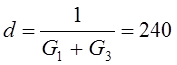                  ,                                Ом.

Соответствующее выражение в среде MathCad 7 Pro выглядит так:

.

Результаты аналитического и численного исследования переходного процесса в рассматриваемой цепи полностью совпадают, по крайней мере до трёх цифр после запятой мантиссы мгновенных значений напряжения резистора u₄(t).

Полученные решения для установившегося напряжения конденсатора u₂(t¢) (переменной состояния цепи Рис. 6.1) для 0 £ t¢ £ T легко распространить на всю ось относительного времени t (–¥ < t < ¥):

,

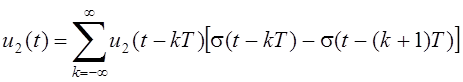поскольку t¢ и t связаны зависимостью (Рис. 6.5):

.

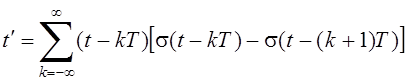Функцию u₂(t) можно использовать в качестве принуждённой составляющей переменной состояния цепи u_2пр(t) при классическом анализе переходного процесса в цепи после коммутации (Рис. 6.1) с источником однополупериодного выпрямленного тока (Рис. 6.2). Выражение свободной составляющей переменной состояния u_2св(t) записываем как обычно:

,

где

 В,

 с^-1.

Существуют и другие методы аналитического решения этой задачи, например, спектральный (частотный) и операторный.

C:\ОТЦиС\Упражнения\Тема_6b\Примеры_6b\Пример 6