«ИССЛЕДОВАНИЕ ОПЕРАЦИЙ»
Задание 1. Решение задач линейного программирования.
1) Составить математическую модель задачи линейного программирования.
2) Решить поставленную задачу графически.
3) Привести задачу к канонической форме.
4) Решить задачу симплексным методом или с помощью симплексных таблиц.
5) Сравнить полученное решение с графическим.
Задание 2. Решение транспортной задачи.
1) Определить, закрытой или открытой является поставленная задача.
2) Если необходимо, привести задачу к закрытой.
3) Определить первоначальный опорный план методом наименьших затрат (минимального элемента) или северо-западного угла.
4) Методом потенциалов найти план перевозок, минимизирующий транспортные издержки, если А - вектор объемов поставок, В -вектор объемов потребления, С - матрица транспортных затрат.
Задание 3. Разработка сетевого графика.
1) Упорядочить сетевой график, если это необходимо.
2) Построить линейную диаграмму.
3) Определить критический путь и продолжительность выполнения комплекса работ.
Вариант 3
Задание 1
Для откорма животных используется два вида корма К1 и К2. В каждом кг корма К1 содержится 5 ед. питательного вещества А и 2,5 ед. питательного вещества В. В каждом кг корма К2 содержится 3 ед. питательного вещества А и 3 ед. питательного вещества В. Известно, что откорм животных выгоден, если каждое животное будет получать в дневном рационе не менее 30 ед. питательного вещества А и не менее 22,5 ед. питательного вещества В. Стоимость 1кг кормов одинакова и равна 1 золотому. Каков должен быть ежедневный расход корма каждого вида, чтобы затраты на корм были минимальными?
Задание 2
А=(9; 27; 19; 19); В=(27; 5; 12);
|
4 3 3 |
|
|
С = |
6 4 3 |
|
6 5 4 |
|
|
4 5 4 |
Задание 3
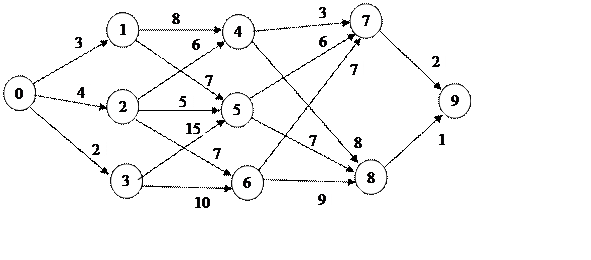 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.